Introduction: Rocket Science ain't all Rocket Science




|
Science sometimes seems far more mysterious than it needs to be. For example, if you asked most knowledgeable astronomers what is involved in determining the required circular orbital speed above a planet or a moon, they would probably begin by trotting out calculus and physics books. Tain't needed, McGee! If you know two basic things you can calculate it using the Pythagorean Theorem! What are these two basic things? Just this: (1) the radius of the planet or moon and (2) how fast things drop at the surface of this planet or moon. That's it! Lets sneak up on the answer with a thought experiment. Let calculate the orbital velocity for just a bit above the Earth's surface. We'll assume the Earth's radius is 3937 miles from the center to the surface. This isn't true everywhere on Earth but this is close enough for what we want to do. We know from experiments that an object drops pretty close to 16' in the first second on Earth. Of course the Pythagorean Theorem is "c²=a²+b²" where c is the hypotenuse and a and b are the other sides of a right triangle. Three noted scientists Jerry Mouse, Tom Cat, and Wile E. Coyote offer to conduct a series of experiments for us. Standing on a platform exactly 16' high, Jerry drops a rock, Tom throws another rock out level with the ground and Wile chucks the rock with a Super Duper Acme Rock Flinger. Jerry notes that his rock hits the ground 16' below him in one second. No surprise there, it is just what we expected. Tom's rock also takes exactly one second to hit the ground from 16' up. After a moment's reflection, the three reason that this is no suprise either. While Tom's rock travels horizontally perhaps a hundred feet or so, it falls vertically exactly the same distance as Jerry's rock or 16'. So both rocks should hit the ground together. However when they time Wile's rock it seems to take just a bit longer than a second for the rock to hit the ground from a 16' height. Tom and Jerry are willing to chalk the itsy bitsy extra time to experimental error, but ole Wile E. Coyote isn't so sure. Reluctantly, Wile hires his old nemesis, the fleet footed Road Runner as his forward spotter. Wile cranks up the old rock Flinger a lot harder and lets fly at a mile per second. Road Runner reports by cellphone that after the full one second the rock is still 3'4" above the ground. What has gone wrong? NOTHING! |
The rock very happily dropped 16' as before, but the Earth is round. A mile from the platform, the Earth's surface has bent an extra 3'4", leaving the rock with just a bit more falling left undone. Wile is fascinated. He keeps winding up the Rock Flinger at increasing speeds. By the time he cranks the old Rock Flinger up until his eyeballs get bloodshot and the rock travels at 4.88 miles per second, something very strange happens. Road Runner reports the rock remains a constant 16' above the ground! Every 4.88 miles, the Earth's curvature bends 16', just enough to keep the rock aloft. The rock keeps going and going and going in low orbit until WHOP! The rocks hits Wile in the back of the head.
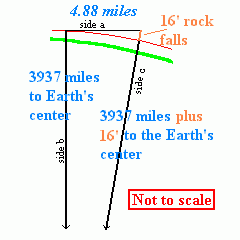 Can we calculate this
mysterious 4.88 miles per second without actually doing these experiments? Sure!
First we convert 16' to miles: 16'/5280' is 0.0030303 miles. The
distance from the Flinger to the center of the Earth (side b) if therefore
3937 miles. At the point where the Earth has dropped away 16' we have to
add back the 16' we dropped to the value we just calculated giving us
3937.0030303 miles (side c, the hypotenuse). Using the Pythagorean Theorem
[c²=a²+b²] we easily calculate the required a=4.88 miles per
second. Since there are 60 seconds in a minute, and 60 minutes in an hour we can convert
this to a more familiar 17585 MPH.
Can we calculate this
mysterious 4.88 miles per second without actually doing these experiments? Sure!
First we convert 16' to miles: 16'/5280' is 0.0030303 miles. The
distance from the Flinger to the center of the Earth (side b) if therefore
3937 miles. At the point where the Earth has dropped away 16' we have to
add back the 16' we dropped to the value we just calculated giving us
3937.0030303 miles (side c, the hypotenuse). Using the Pythagorean Theorem
[c²=a²+b²] we easily calculate the required a=4.88 miles per
second. Since there are 60 seconds in a minute, and 60 minutes in an hour we can convert
this to a more familiar 17585 MPH.
Of course this experiment wouldn't really work in the atmosphere. Friction would slow the rock as it ablated the rock's surface. At these speeds, what you'd create is a horizontal meteor.
Some of you may know that the acceleration due to gravity is about 32'/second². How come we are using 16'? Well at the moment we start to drop the rock it is traveling 0' per second downward. At the end of a second it is traveling 32' per second downward but over the whole interval the "average" is 16' per second approximately.
Just a word of warning for those of you who would like to try this formula on other planets or satellites, or even hundreds of miles above the Earth. The acceleration value we used was measured at the Earth's surface. Other values are required elsewhere. For example, if you inflated the Earth until it bumped into the Moon, without changing the mass of the Earth, the force of gravity would be reduced by the ratio of the Earth's radius to the orbit of the Moon (about 3600 times). If Jerry repeated his experiment on the inflated Earth, he would see the stone drop just about a twentieth of an inch in the first second. Squeezing the Earth results in even weirder problems when you compress all the Earth's mass into something about the size of an acorn. You would generate a black hole. Only some careful application of Einsteinian physics would allow us to describe what would happen to the rock.
Unless you are an incredibly brilliant geometer like Sir Isaac Newton, you will quickly find that using Euclidean geometry to solve complex orbits is totally daunting. Newton did it this way to prove his newly invented Calculus was valid. Since then almost no one tries to do anything but simple circular orbits with geometry alone. Geometry's calculational sibling trigonometry and calculus are the tools of most orbital mechanics. Let see how these play out below.
Part 1: Creating an Ephemeris
Orbital calculations were the very first high precision marriage between mathematics and science. Until the end of the sixteenth century, the idea of creating a mathematics to solve a scientific need had never been considered. Since then science and mathematics have proved fertile grounds for stimulating development in the other. The very regularity of the solar system, the universe's great size and its exquisite conformance to mathematical forms molded the thinking of all great mathematicians even into our own day. At a time when we could not accurately determine how fast a horse could run, astronomers were predicting events centuries in advance to the day, hour and minute. While geometry had been used in architecture and accounting had been used in finance, it was astronomy which created the first need for modern mathematics, a mathematics of motion and change rather than stasis.
A great many excellent programs are now available for personal computers which will allow amateur astronomers to calculate planet, asteroid and cometary orbits with a precision which would have done credit to a major observatory a quarter century ago. However, in this process we have lost a good deal of understanding of what actually occurs in this process. This booklet will attempt to give you a familiarity with the general process that occur within these programs. Inevitably we shall need to use trigonometry, algebra, a bit of vector analysis and we will tread on the borders of calculus. Since we will not be doing proofs even those of you with rusty high school mathematics should be able to follow along the major paths through this booklet. I will introduce the required mathematics just prior to our need to use them.
Before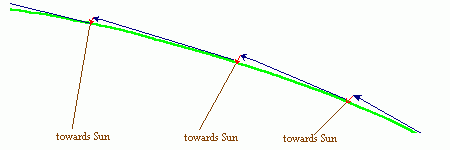 we
leap into trying to understand orbits, lets get a general understanding why gravity
pulling directly towards the Sun results in round orbits rather than simply pulling
everything in the Solar System inwards. If a planet1 was initially stationary relative to the Sun, the Sun's gravity would
pull it directly into the Sun. During the formation of the Solar System, the vast
majority of the material either drifted outwards where the Sun couldn't catch it or fell
directly into the Sun. However some material had a tangential (sideways) velocity and it
began to spin around forming a disk over the Sun's Equator. Fast moving material was able
to maintain itself close to the Sun's gravity. Slower moving material either fell into
the Sun or if it was far enough out was able to maintain itself against the reduced
gravity.
we
leap into trying to understand orbits, lets get a general understanding why gravity
pulling directly towards the Sun results in round orbits rather than simply pulling
everything in the Solar System inwards. If a planet1 was initially stationary relative to the Sun, the Sun's gravity would
pull it directly into the Sun. During the formation of the Solar System, the vast
majority of the material either drifted outwards where the Sun couldn't catch it or fell
directly into the Sun. However some material had a tangential (sideways) velocity and it
began to spin around forming a disk over the Sun's Equator. Fast moving material was able
to maintain itself close to the Sun's gravity. Slower moving material either fell into
the Sun or if it was far enough out was able to maintain itself against the reduced
gravity.
As the planets developed, the residal large tangential velocity remained. Left to itself, this tangential velocity (blue vectors) would have caused the planet to depart the Solar System in a straight line. However during the time the planet goes a short way along this vector, the Sun's gravity will pull the planet a short ways towards the Sun (red vectors). This would result in a ratchet shaped orbit except that as units of time become infinitesimally short, the blue vector would only be an infinitesimal departure from the round green orbit. The red gravity vectors during this momentary period would pull the planet back onto the green orbit. This happens continuously, and the ratchet shape orbit becomes indistinguishable from a perfectly smooth orbit.
Orbital Elements
We will be learning about the nature of orbits. A series of mathematical values called elements are necessary and sufficient to describe an orbit. In some case alternative values can be given, but these alternative values can be used to deduce the ones presented here. The elements are:
|
a
n ω Ω i e |
semimajor axis
mean daily motion longitude of perihelion longitude of the ascending node inclination to the Ecliptic eccentricity |
Shapes of Orbits
 Orbits of an
undisturbed planet about the Sun in four possible shapes, a hyperbola, a parabola, an
ellipse, a circle [or some type of a collision course]. Collectively these are called
conic sections because they all can be produced by cutting a cone with a plane at the
appropriate angle. [Weird ain't it !?] The particular shape involved depends on the
velocity of the planet relative to the Sun. Below a certain minimum velocity any planet
will fall into the Sun.
Orbits of an
undisturbed planet about the Sun in four possible shapes, a hyperbola, a parabola, an
ellipse, a circle [or some type of a collision course]. Collectively these are called
conic sections because they all can be produced by cutting a cone with a plane at the
appropriate angle. [Weird ain't it !?] The particular shape involved depends on the
velocity of the planet relative to the Sun. Below a certain minimum velocity any planet
will fall into the Sun.
- At just the minimum velocity for any type of a stable orbit at a given distance from the Sun, the planet will trace a circle.
- Between the minimum speed and then least velocity required to escape the solar system, the shape of the orbit will be an ellipse.
- At exactly the escape velocity the curve becomes a parabola.
- At velocities greater than escape velocity the orbit becomes a hyperbola.
What is even more amazing is that all of these stable orbits [excluding
the collision courses] can be expressed by a single value, the eccentricity e which
literally means the off - centered - ness of the Sun from the geometric center of the
shape. The Sun always occupies one of the so called foci [focus is the singular] of an
orbit. Only in the special case of a circle does the focus happen to coincide with the
center. The diagram shows the case of an ellipse where the Sun would be located at
f (not at the center as you might expect). If f is at c, then the
orbit becomes a circle. This is very nearly the case for Neptune. 
If you moved f all the way out to a, the ellipse would stretch to infinity and the curve would open on the side opposite a. This is the case for comets which make a single pass through the solar system. If we moved f beyond a, the curve would widen yet again into a hyperbola. This has happened for certain spacecraft which have left the solar system. It also occurs for energetic particles emitted by stars and novae whose orbits pass the Sun appear to be slight bends in otherwise straight lines. This is typical of hyperbolas.
We will have a need to use both cartesian (rectilinear) and spherical coordinate systems because some processes which are difficult in one are simple in the other. For example, switching the origin from the Sun to the Earth is an absolute bear in spherical coordinates but is simple subtraction in cartesian coordinates. Attempting to compute the position of a planet along its orbit is quite simple using spherical coordinates but is a sure fire case of MEGO in cartesian coordinates.
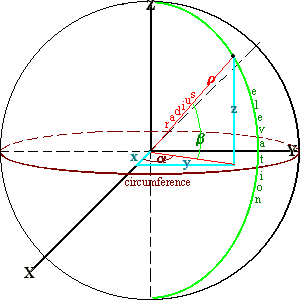
We can easily convert between spherical and cartesian coordinates. Most of the variables in the diagram are the familiar (x,y,z) of the cartesian system or the (α,β,ρ) of the spherical system. Here are the relationships:
| Spherical to Cartesian | Cartesian to Spherical |
| z = ρ sin β | ρ = √(x²+y²+z²) |
| y = ρ cos β sin α | α = tan-1(y/x) |
| x = ρ cos β cos α | β = tan-1[z/√(x²+y²)] |
Kepler's Laws of Planetary Motion
During the last half of the sixteenth century, a Danish nobleman and dedicated astronomer Tycho Brahe [1546-1601] seemed to take a step backwards in science. He rejected the work of Nikolas Kopernicus because he reasoned that a moving Earth would cause a parallax for the stars and none had been detected. [Such parallaxes exists but they are so small they require telescopic cameras and photographic plates to be detected, instruments more than two centuries away].
He made a conscious decision to make careful measurements of the motions of the planets and let the data determine the actual orbits. Until this time the philosophers had relied soly on the human mind, rather than refering to nature to see if what they imagined was true. He can be called the first modern experimental scientist. Before him everyone had been a "natural philosopher". He began compiling positions of stars and planets accurate to an amazing one arcminute with instruments of his own design. Tycho had no access to telescopes which were not invented until seven years after his death by Hans Lipershy and developed by Galileo Galilei [1546-1642]. All of his sightings were by eye.
Tycho recognized his own limitations and hired a young mathematician and astronomer who was forced to leave his teaching position by the Catholic Church. Johannes Kepler [1571-1630] had already been working with planetary positions complied by inferior observers. Kepler found a very fertile field in Tycho's observations.
The two men had a difficult relationship. Kepler was a Copernican, the very system Tycho had rejected. Tycho was afraid and jealous of Kepler's greater mathematical ability but realized he needed the younger man. In an attempt to control Kepler, Tycho dribbled out his results, but ultimately Kepler accumulated enough data to form his three laws of planetary motion. They are:
- All planets travel in elliptical orbits about the Sun with the Sun at one foci.
- Planets sweep out equal areas in equal periods of time.
- Planets travel in a relationship such that the period of the planet squared is proportional to the cube of the planet's distance from the Sun.
Kepler's first law is actually too restrictive. Objects in the Solar Systems travel in orbits which are conic sections, but determining this had to wait for a far greater mathematician - Isaac Newton. Kepler was lucky that Tycho had studied Mars rather than any other body. Mercury's orbit is not exactly elliptical. When this was discovered, astronomers assumed that it was due to the disturbing effect's of an as yet unseen inner planet which they promptly named Vulcan. In fact this slight deviation from an elliptical shape is due to relativistic influences which would not be understood until the early twentieth century by Albert Einstein. Venus has an almost perfectly circular orbit. Deducing any elliptical law from observations which were accurate to an arcminute is not possible. The two known gas giants did not complete enough orbits in Tycho's observations to be adequate.
The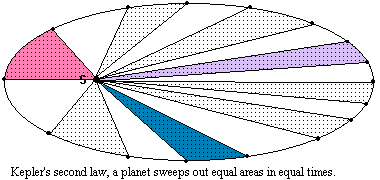 second
law is best understood by examining a diagram. As a planet moves around its orbit, its
speed changes. When it is closest to the Sun (perihelion), its speed is greatest. When
it is as far away as it moves (aphelion), its speed is least. What does hold constant is
that the triangles swept out by the body and the Sun over equal time periods have equal
areas. In our diagram the pink, lavender and blue areas would all have the same area if
the body took the same time to get from point to point. The pink stubby triangle has a
wider angle, but shorter sides. The lavender has a small angle with long sides and the
blue lies somewhere in between.
second
law is best understood by examining a diagram. As a planet moves around its orbit, its
speed changes. When it is closest to the Sun (perihelion), its speed is greatest. When
it is as far away as it moves (aphelion), its speed is least. What does hold constant is
that the triangles swept out by the body and the Sun over equal time periods have equal
areas. In our diagram the pink, lavender and blue areas would all have the same area if
the body took the same time to get from point to point. The pink stubby triangle has a
wider angle, but shorter sides. The lavender has a small angle with long sides and the
blue lies somewhere in between.
Kepler's 2 third law [called the harmonic law in many texts] is generally given as p²=k×a³. p is the period of the planet, a is the length of the planet's semimajor axis and k is a proportionality constant that depends on the units in which p and a are expressed. When p is measured in years and a is measured in AUs (the distance from the Earth to the Sun), k is exactly 1 for objects about the Sun.
Newton's Laws
Isaac Newton [1643-1727] was one of the few true polymaths of all times. He was the greatest physicist, optician, mathematician and astronomer of the late seventeenth and early eighteen century. He was without doubt the greatest geometer of all time. He invented The Calculus, although calculus was also invented by Leibnitz. [Both men were sure that the other had stolen the idea, but in fact each worked independently.] Newton published in 1685 the single greatest work of science the world had ever seen: Philosophia Naturalis Principia Mathematica - The Mathematical Principles of Natural Philosophy [Science]. It literally described just about every branch of exact science with justifications based on mathematics.
To understand the nature of Newton's discoveries it is useful to compare what he was doing with Kepler, Galileo, Hooke, and Halley. Great as these men were they used mathematics descriptively where Newton used mathematics proactively. For example, Kepler found that a curve called an ellipse happens to best describe a set of coordinates of the planet Mars. He had discovered a relationship but had no idea why it was true. Newton worked from the other direction. He lay down a concept of universal gravity and deduced that conic sections [and only conic sections] could possibly describe orbits of two bodies under the influence of gravity alone. Newton understood why Mars' orbit was an ellipse, and what is more he understood why every two body orbit, no matter how fast the bodies traveled was some sort of a conic section. When comparing someone who knows why with someone who knows what, the person who knows why has a much more profound understanding.
Before we go any farther, we need to state Newton's three great laws:
- Momentum A body in motion tends to keep moving in the same direction and a body at rest tends to stay at rest.
- Force If a body is subjected to a force, the force produces a change in momentum of the body in the direction of the force. Simply put f=m×a force equals the mass of an object times an acceleration.
- Reaction For every action there is an equal and opposite reaction. This was a truly inspired understanding by Newton. The first two laws were known in some fashion or other but no one realized Reaction before Newton.
Knowing only Kepler's third law and Newton's second law, it is possible to derive the following equation:
- f = G×m×M÷d²
This is Newton's famous Law of Gravitation. This law applies to any two bodies in the Universe. The story of Newton and the apple falling from the tree is merely an actualization of this law which states that the force of gravity f between any two objects with masses m [apple] and M [Earth] and separated by a distance d squared times a universal constant G. The value of G turns out to be about 6.673×10-11. 3 Certainly the least obvious part of this law says that the action of the Earth on the apple is matched by an equal and opposite reaction of the apple on the Earth. It is totally counter intuitive to realize that the pull of the apple on the Earth is exactly the same pull of the Earth on the apple but in the other direction.
Vis Viva Equation
One of the derivations of Newton's laws of motion has become know as Vis Viva, the Latin name that Newton originally used. It can be translated as the lively force. It is one of the most useful equations in orbital mechanics. Let r be the instantaneous distance between the any two orbiting bodies, then:
- v² = G×(m+M)×[(2÷r)-(1÷a)]
If r happens to always be a, we have a circular orbit. In this case we have the following simplification of the formula:
- v² = G×(m+M)÷r
When a is infinite, the 1÷a term becomes zero and we get:
- v² = 2G×(m+M)÷r
We have just proved a relationship which we have used without proof earlier - the fact that the escape velocity is the √2 times the circular velocity. For the Solar System where the Sun is effectively the only significant mass the formula becomes:
- v = 107225√[(2÷r)-(1÷a)]
This simple formula tells you the required velocity of any body orbiting the Sun, so long as you know its semimajor axis a and its current distance r from the Sun. For example a comet in a nearly parabolic orbit as it crosses the Earth's orbit must be traveling at
- v = 107225√[(2÷1)-(0)] =107225√2 = 151639 kph
The Earth which can be assumed to be in a nearly circular orbit will be loafing along at.
- v = 107225√[(2÷1)-(1÷1)] = 107225√[(2)-(1)] = 107225 kph
| Astronomers are some of the most perverse mathematicians in the world. They absolutely delight in using odd names for common items (like anomaly or argument when they mean angle) and worse yet they are not consistent. Sometimes they use radians, sometimes degrees and sometimes really perverse things like hour angles measure angles in units of time! Worse yet they don't even use the same scales. Sometimes the measurement around what passes for the sphere's equator is -180° to 180° (for example longitudes Earth) and sometimes its is 0° to 360° (positions on the celestial sphere). In like manner the angle from the equator toward what passes for the "pole" may be -90° to 90° or 0° to 180°. We will calculate the "equator" which we will always call the circumference using decimal degrees from 0° to 360°. We will measure the up/down angle which we will call the elevation from -90° to 90°. At the very end of the calculation we will place the circumference or the elevation in a traditional form using traditional units. For example, we will indicate that a circumference is a right ascension measured in hour angles (with 4 minutes to the degree) or that an elevation is an altitude measured from the horizon in degrees |
Calculating an Orbit
 4Lets take a few baby steps before we
leap into the pit. What do we need to know to start? Well, the very first thing we
need to know is where is what are our directions in space anyhow? The X coordinates
lies in the plane of the Earth's orbit at the position of the Sun on the Vernal Equinox.
This is at the intersection of the plane of the Ecliptic and the projection of the Earth's
Equator onto the celestial sphere. Weird as this seems, this place will GREATLY simplify
our lives. The Y axis is 90° counter clockwise in the plane of the Ecliptic
and the Z axis points 90° normal to the plane in the direction of the celestial
north pole. It's difficult described in words but simple when you look at the diagram.
4Lets take a few baby steps before we
leap into the pit. What do we need to know to start? Well, the very first thing we
need to know is where is what are our directions in space anyhow? The X coordinates
lies in the plane of the Earth's orbit at the position of the Sun on the Vernal Equinox.
This is at the intersection of the plane of the Ecliptic and the projection of the Earth's
Equator onto the celestial sphere. Weird as this seems, this place will GREATLY simplify
our lives. The Y axis is 90° counter clockwise in the plane of the Ecliptic
and the Z axis points 90° normal to the plane in the direction of the celestial
north pole. It's difficult described in words but simple when you look at the diagram.
Lets try to make a simple calculation of where planet will be in its orbit, assuming the planet's orbit is a perfect circle with the Sun at the center. We need to know the Sun's distance, which for a perfectly circular orbit is its average distance r. We also need to know how many degrees we rotate in a given time period. Again easy for a circular orbit, we travel 360° over the period p [measured in years] of the planet. Converting to days we have 365.25×p days for our purpose so each day we travel 360°/(365.25×p) per day. However, it doesn't do us much good to know how many degrees we travel per day unless we know where the planet was on a specific date and time [called the epoch designated T0] and how many days there are between the epoch and the moment T we are interested in studying.
This sound like we ought to be able to calculate a fairly accurate orbit for the planet, doesn't it? Well, don't lay any large wagers on your answer just yet. The orbit we will calculate is for a totally fictitious object which the astronomer's call the mean planet - not mean as in nasty but mean as in average. It is only in the same position as the real planet for a brief moment twice a year. Typically we will have an error of many millions of miles.
OK, so why did we bother even trying to start with a circular orbit? Why didn't we just haul out the elliptical orbit equation and use it? Well because there isn't any elliptical orbit calculation which is "closed" - a mathematical term meaning you can solve it neatly. We can only solve it by sneaking up on the answer in a process called convergence. [A less polite, but basically fair, term for convergence is trial and error]. And guess where we start? You got it, with our old friend the circular orbit.
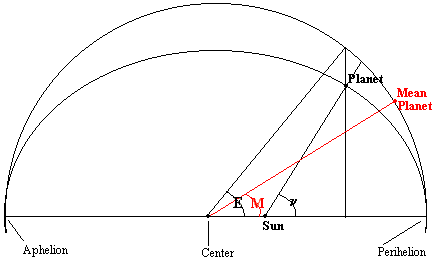 Before we go much further,
lets review what we know. We start with an orbit which is a circle, with the Sun in the
center. Starting at the epoch we measure the angle [called the longitude at epoch
- ω] of the fictitious Earth relative to the starting position at the Vernal
Equinox. We use the mean daily motion as n = 360°/365.25 = 0°.9856. We
designate the current date and time as T. We calculate the position of the mean
Earth and designate it as M.
Before we go much further,
lets review what we know. We start with an orbit which is a circle, with the Sun in the
center. Starting at the epoch we measure the angle [called the longitude at epoch
- ω] of the fictitious Earth relative to the starting position at the Vernal
Equinox. We use the mean daily motion as n = 360°/365.25 = 0°.9856. We
designate the current date and time as T. We calculate the position of the mean
Earth and designate it as M.
- M = ω+(T0-T)×n
The first step to getting a solution was to adjust the position of the mean planet to account for the excess velocity a body has as it passes the closet point to the Sun called the perihelion. [Actually, exactly the opposite case occurs at aphelion where the body has a deficit to make up but we'll ignore this since it is a mirror image solution]. Because of the excess velocity, the planet if it had been traveling in a circular orbit would be at an angle E which is greater than M by a factor of e×sin(E). The sin function is not surprising since it shows up in all sorts of oscillatory motion. Sin(E) is zero at aphelion and perihelion and reaches its maximum value of 1 when it passes the center on its way to aphelion. The eccentricity e scales this term. For orbits which are very nearly circular (those very close to e=0) the effect of the sin(E) diminishes greatly. For orbits approaching a parabola (those almost but not quite e=1) the sin(E) term reaches its greatest potency. Putting it all together we have:
- M = E+e×sin(E)
A bit of rather clever trigonometry reveals that there is a relationship between E and ν as follows:
- ν = 2×tan-1[(√[(1+e)÷(1-e)] tan(E÷2)]
Well you say, doesn't this satisfy the requirements? We have a relationship between E and M and we have a relationship between E and ν. Doesn't this mean we have a relationship between M and ν as we wanted then? No, unfortunately - because the relationship between E and M is backwards. If it had been E=M+e×sin(M), everything would have been fine. But the relationship assumes we know E and e and want to determine M. In fact we know M and e and want to find E. "Well", you say, "don't be a pain. Simply use algebra and solve E in terms of M and e." This sounds great except that this is NOT an algebraic but a transcendental equation. You simply cannot isolate E on one side of the equation with M and e on the other side.
Kepler's equation caused great consternation with mathematicians. It was the first equation they discovered with no closed solution yet described a real situation. The only way to solve for E in the general case, is to propose values for it which converge on the correct solution. Several hundred techniques are known, but they all have hidden pitfalls for the unwary.
The method described here to evaluate Kepler's Equation is based on a mathematical technique called the Newton-Raphson Method which uses the tangent to a curve as a way to rapidly converge on a close approximation to the correct answer. This technique is easily programmed and can even be calculated with a scientific calculator. It normally only takes a few iterations to achieve high accuracy for planets. For values of e near 1.0, convergence is slow.
|
M←(T-T0)×p+ω
E←M e'←e×180.0÷π ε←1÷(10×60×60) repeat
E←E-Δ÷(1-e×cos E) ν ← 2×tan-1 [√(1+e)÷(1-e)×tan(E÷2)] |
We will also want to insure that our answer lies in the range of 0° to 360° at all times. This process is called normalization. If an angle is outside this range add or subtract 360° until the result is in this range. For example M can be many multiples beyond 360° if T and T0 are far apart enough in time.
The tolerance ε is set at 1/10 of an arcsecond. Any tolerance desired may be chosen.
Variables in red are inputs to this function and generally would come from a tables of "orbital elements" for each planet. E and M (in blue) are not needed outside this functions but have geometric significance (see diagram). The true anomaly ν (in green) is the result of this function.
We 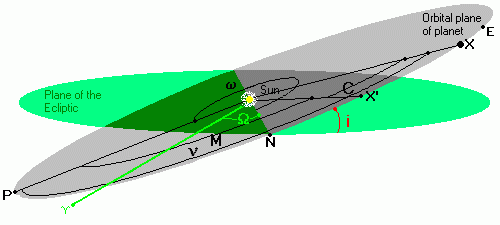 are over the hump, everything else we do is easy in comparison. In
fact, everything else we will do will simply take the result of Kepler's
Equation and display it in some other frame of reference. What we have
calculated is the position of the planet relative to the Sun in the
planet's orbit. As we can see from the diagram we know ν which tells us where the planet lies
relative to the Sun in the plane of the planet's orbit.
are over the hump, everything else we do is easy in comparison. In
fact, everything else we will do will simply take the result of Kepler's
Equation and display it in some other frame of reference. What we have
calculated is the position of the planet relative to the Sun in the
planet's orbit. As we can see from the diagram we know ν which tells us where the planet lies
relative to the Sun in the plane of the planet's orbit.
Lets review what we know:
| p | Daily mean motion |
| a | Length of the semimajor axis |
| T,T0 | Current and epoch date and time |
| γ | Vernal Equinox (First Point of Aries) |
| ω | Argument of perihelion |
To this we now add:
| i | Inclination of the planes of the planet to the Ecliptic |
| Ω | Longitude of the ascending node N |
| Longitude of perihelion6 |
We have calculated:
| M | Mean anomaly of the planet |
| L=ν+M | Mean longitude of the planet |
| C arc X'X" | Equation of the center7 |
| ν=M+C | True anomaly of the planet |
Determining the distance from the Sun to the planet is:
- r = a×(1-e²)
1+e×cos ν
- l = Ω+ν
Projecting Orbital Positions on the Ecliptic
Our next task is to convert from the plane of the planet's orbit to a the Plane of the Ecliptic. [Usually we take the Ecliptic as our reference plane, but for some specialized purposes any other plane may be used for the reference plane].
-
ψ = sin-1[sin(ν)× sin i]
r' = r×cos ψ
l' = tan-1[tan(ν)×cos i]+Ω
To procedure farther, we need to know not only the values for the planet that we have calculated but the equivalent values for Earth. We will distinguish the values for Earth by a subscript e. For example, the distance of the Earth from the Sun is re rather than simply r. There is nothing special about the Earth except that we are assuming that it is our reference platform. If we had been observing from a space craft, we would substitute rsc.
Geocentric Coordinates
The next step requires two slightly differing equations depending on whether the planet is interior to the Earth [or whatever we are using as a reference platform] or exterior to the Earth. We will be determining the circumference λ. The proper name for λ is the geocentric longitude. Test r against re. If the planet is between Earth and the Sun, the r will be less than re and vice versa.
| Case 1: r≤re | Case 2: r>re |
| λ = tan-1( [re'×sin(l'-le')]÷ [r'-re'×cos(l'-le')] )+l' | λ = tan-1( [r'×sin(le'-l')]÷ [re'- r'×cos(le'-l')] ) |
We will also need the elevation β. The proper name for β is the geocentric latitude.
- β =
tan-1[r'×sin(λ-l')÷re×sin(l'-le')]
Are we there yet? Not really. We have come up with coordinates which are geocentric, but they are geocentric in the plane of the Ecliptic. There are two more systems which we will probably want to use - the Equatorial and the Local Horizon systems.
Equatorial Coordinates
| I want to remind everyone that we are using the normalized 0° to 360° system. The Equatorial Coordinate system uses a REALLY PERVERSE idea called hour angles to measure degrees. One degree is equivalent to 4 minutes in this system. It was derived from early astronomers who used the Earth as a stable clock. They were more concerned with when a star or planet would rise, be at the local meridian or set than they were what position it was located. So angles which talk about the Equatorial system divide everything by 15 (360° = 15×24 hours). |
To convert geocentric coordinates to equatorial coordinates use the following formulae
|
α = tan-1 [tan λ cos ε - (tan β sin
ε ÷ cos λ)]
δ = sin-1 [sin β cos ε+cos β sin ε sin λ] |
If you wish to convert α to hour form, divide it by 15. If you want to get it in hours, minutes and seconds, take the fractional part and multiply by 60 twice. [Ugh....]
You may have noticed a cute little ε gizmo which we have never computed before. This is the obliquity [tilt] of the equator to the Ecliptic. It is almost a constant 23°.4392911 as of J2000.0. If you need more accuracy try
- ε = 23.4392911 - 0.0046815J - 0.000000164J²+
0.000005036J³
Local Horizon Coordinates
For completeness, we include the conversion to the local horizon. For the local horizon we need several more bits of information φ the observer's latitude and τ the local sidereal time. We'll assume the you know how to calculateτ(or have a sidereal clock). Your observing latitude should be simple - for example at FDO it is 41°.3671. It can be determined from geodetic survey maps. We will be calculating the azimuth a (circumference) which is the bearing around the horizon starting at North and moving clockwise (so all azimuth numbers are reversed!). The altitude A (elevation) is measured from the zenith 90° down to the nadir -90°.
|
a = sin-1[sin δ sin φ+cos δ cos φ cos (τ-α)]
A = cos-1[(sin δ-sin φ sin a)÷(cos φ cos a)] |
Alternative Methods
There are several major methods which will allow us to calculate the heliocentric position of a body. The more commonly encountered alternatives are described briefly below.
Equation of the Center
If the eccentricity of the orbit is small enough which is the case for the planets, the difference between M and ν (the value C) can be calculated directly from the following formulae:
| C = |
(180÷π)[
(2e - e³÷4+5e5÷96) sin M + (5e²÷4 - 11e4÷24) sin 2M + (13e³÷12 - 43e5÷64) sin 3M + (103e4÷96) sin 4M + (1097e5÷960) sin 5M] |
Direct Computation from Newton's Law of Gravitation
One way is to directly compute using Newton's Law of Gravitation (possibly modified by Einstein's work in extreme environments like near black holes). This technique is extremely computationally heavy because to get good results, the time interval between successive orbital positions must be very close together. Not only must the two bodies principally involved be computed, but every other body in the system. If we decided to only consider the bodies larger than 1000 kilometers, we'd have 17 bodies interacting each with the other - this means we would have to do 355 trillion sets of calculations for each instant, and instants would have to be only a few minutes apart. Even for the fastest computers, this is a staggering computational load.
Mathematicians, programmers and astronomers use various techniques to reduce the interactions. For example, they group all the interactions of Jupiter and its great moons together before they continue. Using this technique, the reduction is huge - over a billion times faster, but it is done at the cost of reducing the accuracy of the final result.
VSOP87
Very good calculations have been made for the solar system for very long periods of time using massive amounts of computing power and Newton's Laws.. To put them into a form which can be used by modest computers these results have been converted into polynomials with more than four thousands terms. These are called VSOP87. Although not as accurate as repetitively solving Newton's Equations, the accuracy of these polynomials is very high. They are used as the basis of the United States and British Astronomical Almanacs. They have been incorporated into several high quality PC programs such as the planetarium programs used at FDO. You may come across VSOP82 polynomials. These polynomials give comparable results, but unlike VSOP87 polynomials they give no clue as to what happens if they are abbreviated which is what is often done to avoid slow running programs.
Abbreviated VSOP87
Besides the high accuracy polynomials, a series of much lower accuracy polynomials have been created. These typically work for a relatively few years (say a couple of centuries) around a useful epoch such as J2000.0. Inaccuracies tend to be far better than the technique described above but do not match the very detailed long range polynomials. These small polynomials cover about 3 or 4 pages in tabular form.
Special Orbits
The orbits above all have one thing in common, they assume that the orbit is ellipitical in shape. While this shape works for a great many orbits it does not cover all the possible orbits of interest. Some additional orbits of great interest are circular orbits, parabolic orbits, hyperbolic orbits, Hohmann orbits and slingshot orbits. The details of these orbits are far beyond the scope of this booklet but they are interesting to understand in general.
Circular Orbits
Circular orbits are probably the most unlikely natural orbits imaginable. They can only occur in an isolated system where outside gravitic influences are undetectable or perfectly balanced such that they cancel one another. Venus has the most nearly circular orbit of any major body in the solar system. Although its eccentricity is very low (about 0.007) it has a detectable value.
Parabolic Orbits
Parabolic orbits arise when the smaller body's velocity is √2 times the circular velocity [the escape velocity]. While this would seem to be a very unlikely velocity, it is precisely the velocity a body would acquire if it fell from an effectively infinite distance. Again this would seem to be an impossible condition, but there is no way to distinguish between a body falling 50,000 AUs and a body falling from infinity. Within our abilities to measure each would be traveling at the escape velocity. In cases where the eccentricity is known to be a slight bit under 1, we often calculate the body as traveling in a parabolic orbit for two main reasons - round off error in the Kepler Equation and using a parabola to represent an extremely eccentric ellipse introduces very slight errors. In fact the errors introduced are often less than measurement errors or accumulated roundoff error in the Kepler process.
Two major changes occur for parabolic orbits (1) the perihelion distance q replaces the semimajor axis a in our calculations and a cubic equation shown below replace the solution of Kepler's equation. Otherwise the calculations basically follow the elliptical descriptions above. The replacement of a with q makes sense because a is expanded to infinity. In the elliptical case, the perihelion distance q exists, it is simply the part of the semimajor axis between the Sun foci and perihelion. In the parabolic case, we simply use the perihelion distance.
The cubic equation which determines the true anomaly is:
- tan³(ν÷2)+3 tan(ν÷2)
-3 [k×(t-T)÷(√2×q3/2)] = 0
Hyperbolic Orbits
Hyperbolic orbits can never occur between the gravity of two bodies acting upon each other. However it can arise in a variety of ways. It is possible for a system of three or more bodies to interact in such a way that the least massive of the three bodies will achieve a hyperbolic velocity - we discuss this a bit more when we discuss slingshots. If a body is accelerated by some force other than gravity, then this body may achieve a hyperbolic velocity. This is precisely what happens when we send a space probe out of the solar system - such as Voyager 1.
Supernovae can eject particles and even clouds of matter at very high velocities. These sometimes enter the Solar System at an angle which causes them to be deflected by the Sun. Even the faster particles of all, light, travel in hyperbolic orbits when they pass the Sun. In fact, a careful measurement of this deflection was detected in 1919 for the first time providing the first substantial verification of Einstein's Special Theory of Relativity.
Local hyperbolic orbit conditions can occur when a rapidly moving object such as a comet passes close to a small body like an asteroid. The comet will leave such an encounter with a slightly altered orbit.
Hohmann Orbits
Consider two planets such as Mars and the Earth. A wide variety of potential orbits can be constructed which will allow you to travel from one to the other. You could attempt to aim directly at the other planet (allowing for the fact that the other planet is a moving target). After firing your rocket halfway you would achieve your maximum velocity at which time you would turn around and begin slowing. You would arrive very swiftly, but your rocket fuel expenses would be staggering. If this is an example of a very expensive (in fuel) orbit, there must be an orbit which takes the least possible fuel to go between worlds. This unique orbit is called a Hohmann Transfer Orbit.
The Hohmann Orbit is an elliptical orbit about the Sun with an eccentricity such that perihelion occurs at the Earth's orbit and aphelion occurs at Mars orbit. All you need to do to travel between the two planets at the least fuel expenditure is to align the major axis of the rocket's orbit such that it touches Earth at departure and will end at Mars on arrival.
Slingshot Orbits
In systems of two bodies, any velocity gained on the inbound leg of an orbit is lost on the outbound leg. However if you have a more complex system such as a major planet moving about the Sun, a small spacecraft may make use of the planet to achieve extra velocity. Effectively, the spacecraft's orbit must be carefully aligned around the Sun such that when it encounters the planet, that it will slow the planet an infinitesimal amount. It does this by transferring some of the planets momentum to itself. This effect is called a slingshot because its resemblance to a "sling of David".
To achieve any useful slingshot effect, a careful alignment is required. However random slingshot effects occur. Occasionally a comet wanders too close to Jupiter or Saturn on its way in or out and has its orbit radically changed. Such slingshots are responsible for short term comets like Halley's or Tempel-Tuttle.
Part 2: Determining Solar Orbital Elements
In this section, we will determine the orbital elements assuming we know certain values for a comet9. The things we will need to know will either be familiar item (such as E the eccentric anomaly) or physical aspects such as the position and velocity of a comet. We will leave to the end of this sections any consideration as to whether such values are easy or difficult to obtain. For now, we'll assume that at some instant of time t, we know the x, y and z distances of the comet from the Sun as well as the velocity of the comet in these three directions vx, vy and vz. We will create two auxiliary variables, the radius r and its velocity vr as:
- r=√(x²+y²+z²)
vr =√(vx²+vy²+vz²)
Calculating the semimajor axis: a
- a=(2-r×vr²)÷r
Calculating the eccentricity: e
- e=√[(1-r÷a)² +(r×vr)²÷a]
Calculating the period: p
- p=a3/2
Calculating the mean daily motion: n
- n=(180*365.25)÷(p×p)
Calculating the eccentric anomaly: E
- E = sin-1[(r√a)]
Calculating the time of perihelion passage: T
We previously we used t0 (epoch), ω (argument of perihelion) and-
M = E-e×sin E
T = t-M÷n
Creating 3 dimensional variables for later use
We assume we know the position of the comet at the instant using standard Cartesian coordinates (x,y,z). We will also need the obliquity of the Earth's orbit ε which we can calculate as we said before. The green calculations and variables are local to this section. The only variables used outside this section are the Ξi and Ψi variables.|
Ux = x÷r
Uy = y÷r Ux = z÷r |
Vx = r×(vx-vr×Ux)
Vy = r×(vy-vr×Uy) Vz = r×(vz-vr×Uz) |
Wx = Vx÷√(Vx²+Vy²+Vz²)
Wy = Vy÷√(Vx²+Vy²+Vz²) Wz = Vz÷√(Vx²+Vy²+Vz²) |
|
Ξx = Ux
Ξy = Uy×cos ε+Uz× sin ε Ξz = Uz×cos ε-Uy× sin ε |
Ψx = Wx
Ψy = Wy× cos ε+Wz× sin ε Ψz = Wz× cos ε+Wy× sin ε |
Calculating the inclination: i
- i = sin-1(√(Ξz²+Ψz²)
- i' = cos-1√[(Ξx
+ Ψy)²+(Ξy-Ψ
x)²]-1
Calculating the longitude of the ascending node: Ω
-
l = cos-1[(Ξx +Ψy)÷(1+cos i)]
u=Ξz÷sin i
Ω=360°+l+u
Calculating the longitude of perihelion: ω
-
v=cos-1[a×(cos E-e)÷r]
ω=u-v
Well it doesn't seem too hard, except that we now have to find the x, y, z and vx, vy and vz values for the comet at the specified instant of time t. So how hard can that be? Well, if you had a very powerful radar, it probably would be too difficult to determine the range bearing and speed of the comet. However, it is a good deal more difficult to solve when what you really have is a series of sightings at a series of dates t1, t2 and t3. These times cannot be too closely spaced, or tiny measurement errors compound yielding very poor results. Effectively what must be done is to determine where the comet is in three dimensions on three dates and to determine the average velocity between pairs of dates and then compute accelerations for each pair of dates as a way to determine instantaneous velocities.
If this doesn't sound to hard, I suggest you read about the discovery of Ceres. Prior orbital calculations depended on many sightings over a substantial part of the object's orbit. However when Ceres was first sighted it was just about to pass into the Sun's glare. Ceres was assumed to be the missing planet that Bode's Law suggested orbited between Jupiter and Mars. Its lose would have been a major problem. Carl Friedrick Gauss came up with a way to solve the orbit of Ceres from just three relatively closely spaced observations. It is an indication of how great his mathematical prowess was presumed that he soon was deemed "The Prince of Mathematicians".
Finally, a minor but real complication comes from the fact that Earth based observations are made using right ascensions and declinations. These observations in and of themselves tell us NOTHING about how far the object is from Earth. A great deal of work is need to tease out the distance from these observations. In fact, the solutions do not yield one answer but three and it is sometimes difficult to see which of these answers is sensible.
Part 3: Determining Orbits of Binary Stars
Hold a perfectly circular loop face on in front of you. I do hope that none of you actually had to run to the closest and sacrifice a perfectly serviceable wire coat hanger. What you see is of course a circular loop. Now tilt the loop so that the top edge moves away from you. Look at the loop and consider what you see. While you "know" that the loop is a circle, the actual image you see is an ellipse. As you continue to tilt the loop's top down, there comes a point where you see a line segment and then finally you see a mirror imaged circle.
Stretch the circular loop into a very elongated (i.e. highly eccentric) ellipse. Now lets try the experiment again with the to bottom. Again tilt the loop so that the top edge moves away from you. What you see is the image of the ellipse becoming progressively less eccentric. At some point you will see the image become circular, then it will become more apparently eccentric along the minor axis. For a moment it become a line segment and then all the shapes reappear in mirror image. By George, you've got it! I really think you've got it! - to paraphrase Pickering as he commented on Liza Doolittle's progress to Henry Higgans.
 The purpose of this mental exercise was to convince you that an
ellipse can appear to be any apparent eccentricity simply by tilting the
proper way. And tilted images is just what we see when we look at
binary stars. For us to do anything meaningful we have to determine the
appropriate orientation.
The purpose of this mental exercise was to convince you that an
ellipse can appear to be any apparent eccentricity simply by tilting the
proper way. And tilted images is just what we see when we look at
binary stars. For us to do anything meaningful we have to determine the
appropriate orientation.
Suppose we come upon a series of dated photographs of a bright yellow and blue binary system. These photographs cover the entire period of the binary system, and even though they were not taken at exactly the same intervals you have a very good selection. If the photographs contain field [background stars] such as we presumably have, you can align photographs to form a composite image.
You may be surprised to see that the photographs do not show one star going around the other. While planets appear to travel around the Sun, the Sun also travels in tiny ellipses around the planets. However, the ellipse the Sun travels is almost impossible to detect because of its huge mass relative to any planet. In the case of binary stars, the relative masses are very comparable. Each star orbits the barycenter (center of gravity) of the two star system. The heavier star will make a smaller ellipse and the lighter star a larger ellipse rather like a seesaw with two children. The heavier child must sit closer to the fulcrum (the barycenter) to balance.
We have a great deal of useful information, but we don't know the true orientation of the binary system. Do we have a situation where the binary system was rotated left to right or top to bottom and how much? If the rotation was around the vertical axis we should compensate as we do with the red arrow on the top. If the rotation was horizontal, we should compensate as we do with the green arrow on the bottom. And we have to remember, that the compensation might be in either direction depending on the orientation of the tilt. A tilt might compound both top and bottom tilts with left and right tilts.
The solution to what might seem an indeterminate problem lies in the very photographs and the dates they were taken. We can determine from the photographs, the speed that each star was traveling by determining the number of degrees covered in an given interval. Stars traveling in nearly circular orbits will have the almost the same velocity at every part of the orbit. Stars traveling in substantially eccentric orbits will travel fastest when the are closest to the barycenter of the system and slowest when they are farthest from the barycenter. We can establish the direction of the major axis by connecting the point of the orbit where the star is traveling slowest to the point of the orbit where the star is traveling fastest.
While its takes a lot of careful work, in essence all we have to do is construct an ellipse which would display the same velocities observed. We can establish the true orientation of the system and its eccentricity.
The general form of Kepler's Third Law [the Harmonic Law: G×(m+M)×p²=4π²×(r+R)3 can help us learn more about this system. We have established the period p and G is a universal constant. From the photograph we at least know the value of r versus R [in this case the yellow star has a semimajor axis twice that of the blue star]. Since we know that r×m must equal R×M we can immediately deduce that the blue star is massive as heavy as the yellow star.
Let assume we have a good estimate of the distance of this pair of stars. Perhaps we have a solid parallax (as we would for a star pair such as Alpha Centauri 1 and 2) on which to base a distance. Or we might know that a yellow dwarf such as we were observing with the magnitude we observed implied a particular distance. In any case once we know the distance we know the diameter of the binary system. This in turn allows us to calculate the velocity of the two stars at any point on their ellipse.
Recall the Vis Viva formula: v²=G×(m+M)÷[(2÷r)-(1÷a)]. If we rearrange the formula we can isolate m+M as: (m+M)=(v²×[(2÷r)-(1÷a)])÷G . Everything on the right hand side of the equation is known, and we have determined that M=2×m. The solution is evident. What is rather remarkable is that we have weighed a stellar system light years away from us with a precision as accurate as our knowledge of the distance.
 Suppose
we had a series of photographs much like the prior example except that
we only observe one star. The star is obviously orbiting a barycenter
in the last case except that we can't see the companion. This might be
the case if the companion was a brown dwarf, a neutron star or a black
hole. We have less direct information with which to proceed because we
cannot directly determine the major axis of the unseen companion.
However we can use an iterative process to converge on a probable ration
of masses and major axes. Unfortunately this process is more subject to
interpretation. Various probable brown dwarfs and black holes still can
provide definitive proof of their existence. New techniques are being
developed to "see" these unseen companions. We can easily detect a
neutron star if it is also a pulsar. Black holes near companion stars
may develop an accretion disk and emit strong x-ray signals. Brown
dwarves are being seen in the infrared from space based telescopes and
large telescopes on high mountains.
Suppose
we had a series of photographs much like the prior example except that
we only observe one star. The star is obviously orbiting a barycenter
in the last case except that we can't see the companion. This might be
the case if the companion was a brown dwarf, a neutron star or a black
hole. We have less direct information with which to proceed because we
cannot directly determine the major axis of the unseen companion.
However we can use an iterative process to converge on a probable ration
of masses and major axes. Unfortunately this process is more subject to
interpretation. Various probable brown dwarfs and black holes still can
provide definitive proof of their existence. New techniques are being
developed to "see" these unseen companions. We can easily detect a
neutron star if it is also a pulsar. Black holes near companion stars
may develop an accretion disk and emit strong x-ray signals. Brown
dwarves are being seen in the infrared from space based telescopes and
large telescopes on high mountains.
For undetermined companions, we might hypothesize that the companion was a small mass orbiting in a large orbit or the opposite, a large mass orbiting in a small orbit. However if we can determine the type of the visible star we can put strong constraints on the possible nature of the companion. For example if the yellow star was a large Cepheid variable, a large orbit (as shown) would completely exclude the possibility that the companion had a low mass. If on the other hand the star was a tiny red dwarf with a small orbit, a brown dwarf might be a reasonable companion choice.
Many binary stars are too close to separate their images. Even if we could barely separate them, attempting to extract orbital information would have a very large margin for error. In these cases, spectroscopic information can often help us determine the orbits. In these cases, while we may not be able to see the stars, we can determine their period and their velocity from the alternating red and blue shifts in the two stars spectra.
Consideration: Binary stars are not easy to calculate accurately. Perhaps 100 such pairs are known to an accuracy of 20%. The distances to most stars is very much in question. Spectroscopic binaries present great obstacles to determining orbital size and shape within a reasonable accuracy. If only one star is visible, it is only possible to establish a lower lit to the stars' combined mass. A number of black hole candidates cannot be conclusively proved to be black holes because only the lower limit to the mass of the visible member is known. For example in a binary system composed of a blue-white giant and an unseen dark companion, a combined mass of 5 sols does not conclusively mean the dark companion is at least 3 sols (although it might be likely).
Footnotes
1 We will use the word planet to mean any object orbiting the Sun including comets, asteroids and even space craft while their rockets are off.
2 The harmonic law can be expressed in completely general terms as : G×(m+M)×p² = 4π²×(r+R)³.
3 The value of the gravitational constant G is notoriously poor. Various modern measurements place the value between 6.6726×10-11 and 6.6739×10-11. The measurement of this value is made with a torsion device called a Cavendish Balance. Most fundamental constants are known to more than a dozen significant digits, while G is accurate to only three to four places.
4 The Vernal Equinox is also called the First Point in Aries, and uses the zodiacal symbol of the ram since this point was established thousands of years ago when it lay in Aries. It now lies in Pisces due to the precession of the Earth's orbit.
5 Throughout the remainder of this booklet, anything in red denotes a caution.
6ω is an alternate
symbol for lowercase π. π is confusing since this symbol is
used for parallax and 3.14159...
7 The equation of the center is the amount the Kepler's Equation adds to M to yield ν. It is called the equation of the center because an alternative method for solving Kepler's Equation for bodies with small eccentricities uses a direct calculation.
8 Just as we previously assumed that the word planet stood for any object in an elliptical solar orbit, we shall now consider the word comet to mean the same.
