Physics for Astronomers
Systeme Internationale (SI) Prefixes
You have almost certainly come upon prefixes from the Systeme Internationale [which is the formal name for the people who maintain the so called Metric System]. Words like kilometer and kilocycles have been used in the United States in spite of our resistance to change. Here are the complete set of size prefixes up/[down] to septillion[th]s.
Name Power Prefix 1/Prefix 1/Power Ten[th]s 10 1 D-deka* d-deci* 10-1 Hundred[th]s 10 2 H-hecto* c-centi* 10-2 Thousand[th]s 10 3 k-kilo m-milli 10-3 Million[th]s 10 6 M-mega μ-micro** 10-6 Billion[th]s 10 9 G-giga n-nano 10-9 Trillion[th]s 1012 T-tera p-pico 10-12 Quadrillion[th]s 1015 P-peta f-femto 10-15 Quintillion[th]s 1018 E-exa a-atto 10-18 Sextillion[th]s 1021 Z-zetta z-zepto 10-21 Septillion[th]s 1024 Y-yotto y-yocto 10-24
* [These should no longer be used but are commonly found (for example a centimeter). The fact that 23n is approximately 10n has led to the odd ball (and fallacious) programming vernacular of megabytes and gigabyte(etc.). The real terms for powers of two to multiples of ten are kibi, mebi, gibi, tibi etc.. A gigabyte is exactly 1,000,000,000 bytes of storage. A gibibyte is exactly 230 [1,073,741,824] bytes of storage. That being said, I still use the fallacious megabyte and gigabyte with wild abandon.]
** [The proper symbol for micro is the Greek letter mu [μ] but it is often shown as the letter u].
In spite of these prefixes, we will often use engineering notation to describe numbers. For some numbers (such as the relative strength of gravity at the 39th power) no prefix has been established. In other cases it will be clearer to show the engineering form.
The older scientific notation is giving way to the newer engineering notation. In scientific notation, a number was a digit followed by an option point and fractional digits of accuracy times ten to a power. Engineering notation has a whole number in the range 0 to 999 followed by an optional point and fractional digits times ten to some power which is a multiple of three. For example 1.273x10-11 (in scientific notation) is 127.3x10-9 (in engineering notion). Engineering notation is converts directly to System Internationale Prefixes.
Fundamental Units
This section only describes the fundamental constants. For the derived and measured constants refer to our astronomy and physics tables or any good reference text on physics or astronomy.
The Kelvin (k°) is the measure of temperature. While not technically correct to say so, we will treat the Kelvin as fundamental. To convert Kelvin to/from Fahrenheit values:
k° = 1.8*(f°+473.15) f° = (k°/1.8)-473.15
For approximate conversions of temperatures in the tens of thousands of degrees simply multiply or divide by 1.8.
The meter (m) is the measure of distance. The English inch is precisely 0.0254 meters.
The gram (g) is the measure of mass (not weight which varies depending on location). An English pound is about 453 grams. Because a gram is a small value, you will often find the kilogram (kg) used in its place.
The second (s) is the measure of time. It is the same in both the English and SI systems.
We will refer to wavelengths and frequencies as if they were fundamental units. They are of course measurements in fractional meters and cycles per second. The word frequency mentioned when talking about the electromagnetic radiation (called light in this booklet). The measure of frequency is the hertz(hz). Light has wavelike attributes that look like a chain of wiggles (a sine curve for purists). If 50,000 wiggles pass a point in a second, the light has a frequency of 50 kilohertz. Light can also be measured by its wavelength. The formula relating the wavelength to the frequency of light is:
wavelength = c/frequency.
The Four Forces
All force in the universe comes in one of four forms: gravity, light, the strong nuclear (SNF) and weak nuclear (WNF) forces. We will not consider the weak nuclear force since it has little or no bearing on astronomy. It is of interest primarily in studying certain forms of radioactive decay.
Gravity
particle : graviton (hypothetical, not yet actually found) range : infinite properties : pulls (never pushes, i.e. no antigravity) strength : About 10-39 SNF.
Gravity is the real mystery force because it is so weak. The weaker the force, the more powerful the tool must be to demonstrate the particle. To date we have never measured a gravity wave front much less measured a single gravity quanta.
We use the Newtonian definition of gravity for most astronomy work. In this case, gravity is a force attracting two bodies towards each other at a rate proportional to the product of their masses. We won't get into Einstein's relativistic gravity or attempts to create a quantum physics gravity.
Light (Electromagnetic Radiation)
particle : photon range : infinite properties : positive and negative charges, polarization strength : About 1/100-10-6 SNF*.* This value depends on the range. At subatomic distances the effective strength is not shielded by so called virtual photons.
Electromagnetic radiation is called light) in this booklet even if it is outside the visible light spectrum. At its lowest frequency, light is long radio waves and at its highest frequency it is gamma radiation.
spectrum : radio mwave IR visual-light UV X-ray gamma wavelength : longest ......................... shortest frequency : lowest ........................... highest structure : wavelike ................... particle like energy : "soft" ............................."hard"
[Strong] Nuclear Force
particle : gluon (demonstrated, but never isolated) range : about the size of an atom's nucleus (very short) properties : binds nucleus fiercely, spin is akin to polarization strength : 1039 gravity and 106 light.
This is the ultra heavy weight champion of the universe when it comes to forces. Only one thing keeps it from overwhelming gravity and light, it has a particle which cannot be pulled much more than the diameter of a large atom. The nuclear force doesn't even reach as far as the innermost electron. However, when an atom is split or fused, some mass is lost because of the nuclear force. Small as this mass is, it produces a huge amount of energy as we see from Einstein's famous:
e = m c2
Even a tiny mass when multiplied by c2 (about 90x1015 m2/s2) is a huge amount of energy. One tiny gram's worth of energy could hurl FDO out of the solar system at a huge velocity if it didn't pulverize it first.
Weak Nuclear Force
particle : Tau muon range : about the size of an atom's nucleus (very short) properties : similar to light, causes radioactivity. strength : similar to light
Except for the radioactive decay of certain elements created in the center of stars and supernovae, the weak nuclear force will not play a role in our discussions.
Elementary Particles
We are studiously avoiding about the last third of a century of nuclear physics. We are not talking about quarks or mesons or any of the other weird denizens of modern physics. We are talking about atoms as most scientists thought of them circa 1965 - things composed of protons, neutrons and a cloud of electrons. Well here goes:
Electron
An electron can be thought of as a cloud like thing containing a negative electric charge. Do not think of an electron as a point circling the nucleus. When an electron is attached to an atom, it occupies a layer (called a shell) above the nucleus. Its exact location cannot be pinned down so it appears as a kind of a cloud. Another kind of positively charged electron (positron) is created when a star fuses hydrogen or helium to create energy. If an electron meets a positron, their opposite charges attract and they collide creating a quanta of light at the most energetic part of the spectrum - a gamma photon.
Proton
A proton is a positively charged particle. It is found in the nucleus of an atom. In normal situations, every proton is balanced by an electron in a shell above it. Artificial protons can be created with negative charges. They do not play any role in this discussion. In certain nuclear reactions - such as the fusion of normal hydrogen to form heavy hydrogen (deuterium), a proton can emit a positron changing the proton to a neutron. The positron immediately encounters an electron, annihilating both and producing an energetic gamma ray.
Neutron
Neutrons are electrically neutral particles which make up an increasingly large percentage of an atom's nucleus as we move towards the heavy end of the periodic table. Very roughly speaking a neutron is a proton which has swallowed an electron to become electrically neutral. Neutrons are required to allow the nuclear force to hold the protons together.
All neutrons outside the nucleus are unstable. After about 15 minutes or so, they break down into a proton and an electron. An atom which consists of a single proton and a single electron is the most common atom in the universe - hydrogen.
In some nuclear fusion reactions, a neutron will emit an electron. For example a neutron in beryllium can emit an electron changing the element to lithium.
Neutrons can be held together in a gigantic nucleus miles across if a sufficiently large gravity field is present. We call this stuff neutronium and it is one of the possible fates that can affect a star.
Neutrino
The neutrino is a charge less and probably mass less particle whose main function is to conserve momentum when fusion takes place. There are three flavors of neutrinos, but we won't discuss them further. My only reason for mentioning this beasty is that about 8% of the stars radiation escapes this way. Neutrinos are really antisocial. They can travel through light-years of lead (or anything else) without interacting with any atoms of lead. Effectively matter is almost perfectly transparent to neutrinos.
Absorbtion and Emission
Electrons and photons interact very strongly. If a quantum of light
which is sufficiently strong, it can "kick" an electron from its current shell to a higher
one. At some time later (from microseconds to hours) the atom can relieve the strain by
allowing the electron to fall causing a quantum of light to be emitted. In some cases,
the initial quantum of light may be strong enough to "kick" the electron up multiple
levels. When the electron subsequently falls, it may fall one, two or all of the levels.
If it falls in small steps, low energy light photons are released. If it skips and falls
several levels at a bound, high energy photons are released. Sort the following:

As we shall see, nuclear fusion in the Sun creates the most energetic form of light - gamma radiation. As the gamma photons try to force their way out of the Sun's core they encounter countless electrons orbiting atoms. Time after time they interact. Sometimes they spit out the gamma photon, but more likely they spit out several X-ray and ultraviolet photons. In turn these cascade down through additional countless atoms become the entire spectrum from the radio frequencies to ultraviolet light. Except under unusual conditions like a solar flare occurring during a space mission, the dangerous x-rays and gamma rays do not reach the surface except in tiny amounts.
Atoms, Isotopes, Ions and Molecules
Atoms, or more correctly electrically neutral atoms, consist of 1 to 92 (or more for man made atoms like plutonium) protons mixed with 0 to 146 neutrons. If an atom's nucleus has a certain number of protons say 6 [carbon], then to be electrically neutral it must be surrounded by 6 electrons. If you see the atomic symbol written as nLm the letter "n" specifies how many protons are in the atom, the letter "L" is just to help us remember what an "n" proton atom is chemically, and the "m" is the total number of nucleons [protons plus neutrons] in the atom. So 6C12 is ordinary Carbon. Since ordinary Carbon has 6 protons and 12 nucleons all together, it must also have 6 neutrons. One atom, ordinary Hydrogen comes in a form with NO neutrons (the only atom that doesn't have at least neutron 1H1.
An isotope of an element is one where the number of protons are equal but the number of nucleons varies between two types of the same chemical. For example, 6C14 is the slightly radioactive form of Carbon which we use for radiodating fossils of living plants or animals. 1H2 is the "heavy water" form of hydrogen which we call deuterium which powers H-bombs. 92U238 is ordinary Uranium - radioactive but non explosive while 92U235 is the stuff which blows up in bomb.
So far we have been talking about the nucleus of an atom. Electrically neutral atoms have as many electrons as the leading subscript number. However, it is fairly easy to strip one or more electrons from an atom. We all own devices which are designed to do this - we call them TVs. Heat, light, electrical and magnetic fields can all be used to pull the electrons off. What remains is a "charged" ion. Normally, the nucleus grabs the next free floating electron it can find, but if it is alone in space or in the heart of a star, conditions prevent this and we get a soup of ions we call a plasma. Plasmas are often incorrectly called a gas. They aren't! Gasses are nonconductors of heat and electricity. Plasmas are far better conductors of heat and electricity than any metal.
Inside every atom [except 1H1] there is a battle between the repulsive electromagnetic and the binding nuclear force. The nuclear force isn't enough in large atoms composed solely of protons. The additional nuclear force is supplied by neutrons. Neutrons add no repulsive electromagnetic force, but they do add binding nuclear force. However nuclear force is very short range. If too many neutrons are added, the nucleus' diameter exceeds the binding range of the nuclear force. The cores of atoms are constantly squirming about. Sometimes the atoms squirm into elongated shapes where part of the nucleon lies outside the binding energy field. The atom breaks apart in a reaction called radioactive decay. When atomic nuclei hit each other at high velocity, violent changes in nuclear shapes occur and atoms can split apart or fuse together.
Molecules are chemical bonds between atoms. Most atoms will yield, accept or share electrons to form completed outer shells. The exceptions are the so called noble gasses [Helium, Neon, Argon, Krypton and Radon] which have completed outer shells as is. Many atoms can combine with themselves. For example, hydrogen gas is really composed of pairs of hydrogen atoms shared together as hydrogen molecules. When molecules lose electrons as can happen in thin interstellar passes they form something known as free radicals. Free radicals are highly reactive chemicals that bind very readily.
Spectrographs
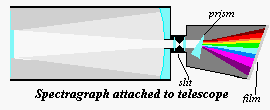 No telescope attachments
other than the eyepiece and the camera [film or CCD] has been as crucial to astronomy as
the spectrograph. Essentially the spectrograph is a device which takes the light from a
telescope, sends it through a slit (with the aid of collimating lenses), then through a
prism [or a ruled grating] into a camera body [film or CCD].
No telescope attachments
other than the eyepiece and the camera [film or CCD] has been as crucial to astronomy as
the spectrograph. Essentially the spectrograph is a device which takes the light from a
telescope, sends it through a slit (with the aid of collimating lenses), then through a
prism [or a ruled grating] into a camera body [film or CCD].
 What is produced is a
spectrogram composed of a rainbow crossed by numerous dark bands. The bands come in two
forms dark absorption bands and bright emission bands. The dark bands are caused when
light passes through cold gas which traps a particular wavelength for that particular
atom. In the case above, we see this as the prominent alpha and beta lines of hydrogen.
If the gas is heated (excited) to a point where the gas shines at a particular frequency,
the situation may reverse itself and we get light emitted at that specific frequency.
What is produced is a
spectrogram composed of a rainbow crossed by numerous dark bands. The bands come in two
forms dark absorption bands and bright emission bands. The dark bands are caused when
light passes through cold gas which traps a particular wavelength for that particular
atom. In the case above, we see this as the prominent alpha and beta lines of hydrogen.
If the gas is heated (excited) to a point where the gas shines at a particular frequency,
the situation may reverse itself and we get light emitted at that specific frequency.
An astounding amount of information can be obtained from a spectrograph. Each band seen in the heavens be reproduced in the laboratory. They are the finger prints of the elements of the periodic table. We can know the chemistry of the stars with great confidence at huge distances. The second most common element in the universe, helium, was identified in the Sun's spectra (hence the name) long before it was found in deep natural gas wells.
When a star is moving towards or away from the solar system, the spectral bands shifts towards the red or blue [actually violet] ends of the spectrum. Stars moving towards us have a blue shift. Stars moving away have a red shift. The speed of the star is easily deduced by the amount of the shift. Many significant facts can be deduced by lines shifting.
Distant galaxies all move away from us and each other. All of their spectra show a red shift. This is the best evidence we have that the entire universe is expanding.
Very close binary stars will each have their own spectra. Suppose the first star happened to have a prominent line for sodium and the second star happened to have a prominent line for carbon. When the sodium lines is bluer than normal, the carbon line will be redder than normal. Sometime hours or days later we will see the opposite case: the carbon line shifted towards the blue and the sodium line shifted towards the red. The time between these shift is exactly the time for the stars to complete half a rotation about their orbit. Knowing this we can deduce the stars' masses, distance and orbital size and shape. Combined with the colors of the stars (also from the spectrograph), we can deduce the life history of the stars.
Sometimes the lines come as pairs, slightly separated. This effect is caused by strong magnetic fields. Again the spectrograph gives us unexpected information.
Some modern spectrographs bypass the camera and directly examine the spectral bands by a CCD and computer software. Digital techniques can be useful in matching spectral bands which are highly shifted.
Recently Delta Scorpii [Dschubba] erupted brightening by about half a magnitude. One very significant change was that the spectrum changed from an absorption to an emission spectrum. This means that the upper layers of the atmosphere of the star are no longer absorbing light emitted from lower layers but are emitting light of their own. The mechanism is probably akin to what happens in a neon or mercury vapor lamp. High frequency radiation (ultra violet or X-rays) excite atoms in the star's upper atmosphere. The electrons are boosted from lower to upper orbits. When they electrons fall back to normal shells, light is produced at the specific wavelengths appropriate for that atom. Effectively, Dschubba has changed temporarily from a B IV [blue giant] to a Be [emission] giant star.
If the spectrograph has any major fault it is that the very process of creating the spectrogram smears light across a surface rather than collecting it at a point. For moderately bright objects this is not a matter of concern, but for dim objects it means that very large telescopes are required to collect enough light.
Air Ball, Air Ball!
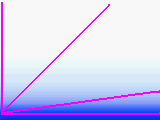 All though it varies with
the weather and the season, a vertical column of air from sea level to far outer space
contains about the same amount of air as a horizontal column of air about 5.25 miles long.
Air thins rapidly on Earth, for as you climb, the air halves every 3.6 miles on average.
If you were in a jet at normal cruising altitude better than 3/4ths
of the atmosphere is below you. At 25 miles up 99% of the atmosphere lies below you.
NASA lists anyone who has reached an altitude of 50 miles as an astronaut. Why not, there
is almost no air to speak of up there.
All though it varies with
the weather and the season, a vertical column of air from sea level to far outer space
contains about the same amount of air as a horizontal column of air about 5.25 miles long.
Air thins rapidly on Earth, for as you climb, the air halves every 3.6 miles on average.
If you were in a jet at normal cruising altitude better than 3/4ths
of the atmosphere is below you. At 25 miles up 99% of the atmosphere lies below you.
NASA lists anyone who has reached an altitude of 50 miles as an astronaut. Why not, there
is almost no air to speak of up there.
We live in an air ball. Take a look at the diagram which is as close to accurate as I can draw with MSPAINT. Most of the air is close to the surface. The dense atmosphere occlusion decreases rapidly with altitude above the horizon. A star at 45 degrees passes through little more air than a star at the zenith. For most situations, try to avoid targets which are less than 15 degrees from the horizon. If you sight a star on the horizon, it has to travel through about 13 times as much air as a star at the zenith. Although air has a very low index of refraction, that much air acts as a very powerful lens. This causes objects just below the horizon to be lifted to just above the horizon. The approximate formula is
a' = a + 0.016*tan(90-a)
where a (and a') is the altitude in degrees. For example a star 1°1 above the horizon appears about 1°55' above the horizon.
a' = 1.0+0.016*tan 89.0 = 1.0+0.016*57.29 = 1.916 [1°55']
This error is almost twice the diameter of the Moon. The error gets even worse if the weather has a temperature inversion (a warm layer aloft). Errors can reach several degrees with inversions active.
Five Reference Systems
Each reference system has two basic angular measurements, a longitude
(360°) and a latitude (180°). When required, an additional measurement - the
distance can be added. Usually the distance is called the radius. We could use Cartesian
coordinates, but for our purposes, spherical coordinates are more intuitive and simpler to
describe. One of the peculiarities we shall see is that the longitude is often measured
in unusual terms such as hours (a hour is 15°) or with unusual signs such as East and
West. One critical place in the sky is the vernal equinox (also called the first point of
Aries for historical reasons). It is denoted normally by the zodiacal sign of the Aries
 . This is the point where the plane of the Ecliptic and the
Plane of the Earth's Equator cross as the Sun appears to move North on its yearly cycle,
i.e. the start of Spring. We need three systems for solar astronomy Alti-Azimuth,
Right Ascension/Declination and Ecliptic, we use another for positioning
ourselves on the Earth (Equatorial ) and finally we sometimes use the plane of the Milky
Way for refereeing to stellar motions (Galactic).
. This is the point where the plane of the Ecliptic and the
Plane of the Earth's Equator cross as the Sun appears to move North on its yearly cycle,
i.e. the start of Spring. We need three systems for solar astronomy Alti-Azimuth,
Right Ascension/Declination and Ecliptic, we use another for positioning
ourselves on the Earth (Equatorial ) and finally we sometimes use the plane of the Milky
Way for refereeing to stellar motions (Galactic).
Alti-Azimuth
The Alti-Azimuth spherical coordinate system (also know as the horizon based system) displays the sky in terms of the viewers local position on the Earth. A satellite which was directly overhead at the North Pole, would be on the horizon for a viewer on the Equator. This system accounts for this positioning.
Longitude or Azimuth:
0-360° measured clockwise from due North. (N-0°; E-90°; S-180°; W-270°)
Latitude or Altitude:
-90° - 90° measured from the nadir (-90°) through the horizon (0°) to the zenith (90°).
Radius:
Hardly ever used except in parallaxes, but it is the distance to the center of the Earth.
Right Ascension (RA) and Declination (Decl)
The RA/Decl system is an outgrowth of navigation where it was easy to measure the angle of Polaris, but where distances East and West were unmeasurable until very recently. Clock times were used to calculate when a star would rise or set. Since the world turns 360° in 24 hours, each hour angle is 15°.
Longitude or Right Ascension:
0-24h measured clockwise from  .
Convert hour angle to degrees for calculations.
.
Convert hour angle to degrees for calculations.
Latitude or Declination:
-90° - 90° measured from the south to north celestial poles (Polaris and Octans)
Radius:
Distance from Earth to the solar system body or star.
Equatorial System
The Equatorial System is familiar to everyone who has looked at a map of the Earth. It is the familiar meridians that measure North/South and East/West. This system is closely tied to the RA/Decl system since they both use the plane of the Equator as a common reference.
Longitude:
180° West 180° East Note: west means negative numbers.
Latitude:
90° South to 90° North . Note: south means negative numbers.
Radius:
Almost never used, but the distance from the center of the Earth to the surface.
Ecliptic System
The Ecliptic System uses the plane of the Earth's orbit about the Sun as the reference. The center is the center of the Sun. This system is used for all solar system calculations that describe planets, asteroids and comets in relation to the Earth.
Longitude:
0° to 360° measured from  .
.
Latitude:
-90° to 90° measured from the south celestial pole. You can determine north by applying the left hand thumb rule aligning the fingers to the direction of the Earth's motion.
Radius:
This is the distance from the Sun to the body.
Galactic System
The Galactic System uses the plane of the Milky Way as the reference. This system is useful when discussing the proper motions of stars about the Milky Way's hub. The hub is the center.
Longitude:
0° to 360° measured from  .
.
Latitude:
-90° to 90° measured from the south galactic pole. You can determine north by applying the left hand thumb rule aligning the fingers to the direction of the Sun's motion about the hub.
Radius:
This is the distance from the hub to the star in question.
Three Classical Laws
Newton's Universal Gravitation Law
Given two bodies interacting gravitationally with masses M and m, then the force of gravity F can be determined from
- F = G*M*m/d2
This law has an alternate derivation based on Kepler's third law of motion which states that the period of a planet squared is equal to the cube of the planet's semimajor axis: P2=a3. Useful as Kepler's Law is, it is too simple. First of all, it only applies to the Sun and the planets. It doesn't work for Jupiter and its moons nor for binary stars - at least without a lot of tinkering. Newton correctly rewrote Kepler's third law as:
- (m+M)P2 = K(a3)
The reason that Kepler's approximation worked at all was the M (the mass of the Sun) was huge compared to m (the mass of each planet). No matter what planet was selected the total was equal to M to much better than an accuracy of 1% which was all Kepler's data would permit. When you choose the semimajor axis in astronomical units (AUs) and the period in years, the value of K is one.
Let go a little further and get an idea how this equation allows us to calculate the mass of a each member of a binary star. We'll assume that the masses of the two components are m and m respectively. Suppose a binary pair was located 2.67 parsecs away. [We'll use parsecs because we'll be multiplying by arcseconds.] After watching this system for decades we determine that angle between them averages 7.5 arcseconds and it takes 50 years to complete an orbit. We also observe that one star makes a orbit which is have the diameter of the other star. Given the distance and the angular separation we can determine that these stars are 20 [2.67*7.5] AUs apart. This gives us:
- m+m = (203/502) = 3.2 solar masses
Given the ratio of the two orbit sizes, the larger star is about 2.1 solar masses and the smaller star is about 1.05 solar masses.
Warning, this example grossly simplifies the effort. For example if the plane of their axis is not perpendicular, a fairly tricky bit of geometry is needed to determine the true as opposed to the foreshortened elliptical shapes. These stars aren't hypothetical but are Sirius A and B.
Wein's Law
A blackbody is a theoretically perfect (ideal) aborption and radiation mass. If the surroundings are hotter, a blackbody absorbs 100% of the light which falls on it. If the surroundings are cooler, 100% of the excess thermal energy is converted to light. Opaque gas turns out to be a very good approximtaion to a blackbody. In turn the overwhelming bulk of most stars emits radiation like a blackbody of a similar surface temperature.
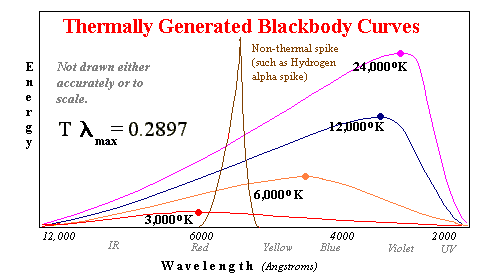 Blackbodies can be
studied in the laboratory. It turns out that two measurements at different wavelengths of
the intensity of light are sufficient to determine which blackbody curve is correct.
Using filters, we can measure a red frequency and a blue frequency and determine with
great accuracy that the maximum intensity wavelength is yellow or ultraviolet even if we
can't measure that frequency.
Blackbodies can be
studied in the laboratory. It turns out that two measurements at different wavelengths of
the intensity of light are sufficient to determine which blackbody curve is correct.
Using filters, we can measure a red frequency and a blue frequency and determine with
great accuracy that the maximum intensity wavelength is yellow or ultraviolet even if we
can't measure that frequency.
Stefan-Boltzmann Law
One more of laboratory law is needed to complete our tool kit. It says that energy emitted per square meter is proportional to the FOURTH power of the temperature.
- ET = 56.72x10-6 T4
Although these three relationships may not seem like such a big deal, together they allow us to determine a star's type, its mass, its temperature, its rate of energy production, its diameter, its life expectancy and its future fate. For example, if a larger star is twice as massive as a smaller star and the larger star is five times as hot as the smaller star then the larger star will only live about 1/1000th as long as the smaller star.
Apparent and Absolute Magnitude
If we look at the Sun, it appears to be trillions of times as bright as any other star. We know of course that this is do to the fact that it is only 8 light minutes away from us rather than many light years away from us. All stars (even the Sun) have an apparent magnitude which means how bright it appears to us.
Since how bright a star appears to us is accidental and depends on that star's distance it is much handier to create a standard distance (ten parsecs or 32.6 lightyears) and to calculate how bright the star would appear if it was at the standard ten parsec distance. Our Sun which appears to be a dazzlingly -26.5 magnitude would be a dim 4.8 magnitude star at ten parsecs.
Norman Pogson proposed that we define stellar magnitudes in such a way that a first magnitude star was 100 as bright as a sixth magnitude star. Each magnitude therefore represented the fifth root of 100 or a number about 2.512. So if two stars differed in magnitude by 3 then the brighter star would shine 15.8 times as brightly as the dimmer star. That is as true for a magnitude 0 and 3 star pair as for a magnitude 4 and 7 star pair.
Imagine the Sun shinning onto imaginary spheres centered on the Sun. If one sphere was 1 AU from the Sun [near Earth] and another was 5 AUs [almost to Jupiter] then the Sun's intensity on the smaller sphere would be 25 times the intensity on the larger sphere PER SQUARE METER. The reason is simple, the larger sphere has 25 times as many square meters on its surface than the smaller sphere and the same amount of light must cover 25 times as much area.
A star which is ten times as far way as an identical star would be 100 times dimmer or 5 magnitudes.
Color and Temperature
Up to this point we have been alluding to a relationship between the color of a star and its temperature. Our first problem is to define what we mean by color on a numerical scale. One way would be to simply indicate the number of nanometers in the principle wavelength, but it doesn't let us establish what that wavelength is. There is a specialized instrument which works for sufficiently bright stars (a bolorimeter) but we will use another method, observing the star through three filters (an ultraviolet "U", a blue "B" and a greenish-yellow "V"). The greenish-yellow or visual filter is designed to pass the maximum light at frequencies optimal for human night vision. The three filters must be sufficiently dense that they all allow exactly the same amount of light to pass when viewing Vega (or any other bright star with a surface temperature of 10,000°K.
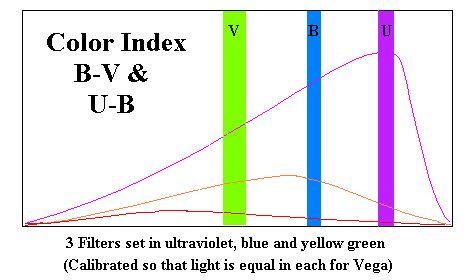
I know of no formula for converting color indices to temperature but the following chart is approximately correct.
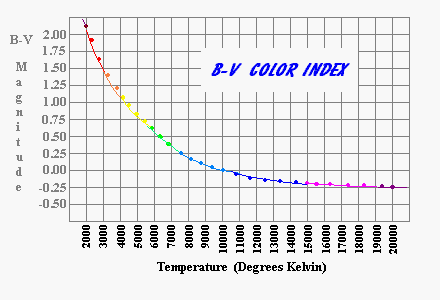
Spectral Classes
Just before World War I, a Danish astronomer Ejnar Hertzsprung ran a comparison of the colors and luminosities within globular clusters. Even though the distances to the clusters were on crudely known, Hertzsprung knew that all stars in the clusters were approximately the same distance from the Earth, so that the relationship between color and luminosity was valid. Meanwhile an American astronomer Henry Norris Russell ran basically the same relationship on stars close enough to have their distances measured trigonometrically. When the color index was plotted against the magnitude (adjusted to a standard distance) most stars fell within a lazy S curve we now call the main sequence. In general red stars were dim and blue-violet stars were brilliant. However two odd outlier groups were found. Some red stars were extremely brilliant and some very blue-white stars were exceedingly dim.
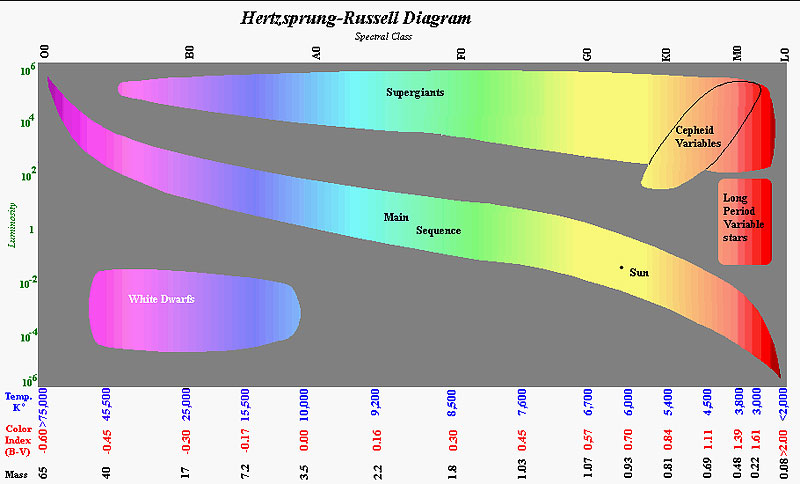
The Sun is about 5800°. A star with a temperature of 3400 degrees (a very red star) radiates at only (3400/5800)4 (10%) of the Sun's rate per square meter. This relation fit very well with the nearby stars whose mass was known to be small and whose energy production was correspondingly small.
However some stars like Betelguese and Antares are known to be distant, very bright and they are certainly red. The only way a dim bulb can shine with a great deal of light is for that dim bulb to be huge. Stars like Betelguese or Antares radiating at one tenth the Sun's rate must be hundreds of million kilometers in diameter to be so bright.
When Sirius B was discovered in 1862, the opposite condition prevailed. Sirius B is blue-white (B-V = -0.11) implying a temperture of 12,000°K. If it was as large in diameter as the Sun it should radiate at an absolute luminosity 30-40 times the brightness of the Sun. Instead of a star with an apparent magnitude far brighter than Venus, it is 10 million times fainter than Venus. The only way something that radiates as intensely per square meter as Sirius B does yet is intrinsically dim is for the star to have a very small radius on the order of 1% of the Sun's diameter [about the diameter of the Earth]. Newton's Universal Law of Gravitation allows us to take observations of Sirius A and B positions and velocity and from this deduce the masses of both stars. Sirius B is 5% heavier than the Sun. This means that Sirius B was almost 100,000 times as dense as the Sun.
A star's color combined with its brightness and distance tells us most of what we know about stars. There is a direct relationship between the color and the temperature of the star. The exact values are not important to us, but they range from about 2300° Kelvin for brown dwarves to over 70,000° Kelvin for the ultra fast burning ultraviolet giants. The temperature of the star tells us how fast the star must consume its hydrogen. It is a fourth power relationship so the hottest stars burn fuel at more than 800,000 times the rate of the coolest stars. Typically, the hottest stars are no more than 500 times the mass of the coolest stars. This means the hottest stars last less that 1/1500 the life span of the coolest stars.
The star's spectral classes are show as a letter with a roman numeral following to specify what size star it is. A red star (M class) can be a small slowly burning star or a nearly burnt out giant star so the qualifying roman numeral is crucial. It would make sense if the classes were ordered alphabetically, but for a variety of reasons they don't.
The spectral classes are O, B, A, F, G, K, M, L [R, N, S]. The jingle Oh, Be A Fine Girl, Kiss Me Lass! Right Now! Smack! was created by Henry Norris Russel. The last three letters (R, N and S) are K and M like stars with many heavy element lines in their spectrums. The letter L was just added in 1999 when the first brown dwarf was detected and confirmed.
In addition, to the spectral class letter and the roman numeral size qualifier, stars have a spectral class refiner. For example the Sun is a G2V star saying that it is a bit warmer than a standard G star (at 5800°Kelvin) and that it is a yellow dwarf (meaning it is not a giant).
Spectrographs
The spectrum of light has dark bands which are the signatures of various atoms. For example Hydrogen has a red line which is either very brilliant if the star is emitting or is a dark line if intervening gas is absorbing.
The positions of these dark bands is very precisely known. If a body is approaching us its light shift these dark bands towards the blue end of the spectrum. If it is receding, it shift the bands towards the red end of the spectrum. These shifts can be used to establish the expanding universe (red-shift).
Another use is for measuring the speeds of stars as they orbit each other. Some double stars are accidental alignments of a foreground and a background star. These are called physical doubles. Some stars are widely enough separated to be seen as two distinct stars. These are optical doubles. Some stars can only be determined as double by the fact that they have minutes shifts in the bands. These are called spectrascopic doubles. A refinement of spectrascopic searchs for doubles has allowed us to actual detect planets around at least 20 stars.
Types of Stars
Stars come in many types from dwarfs (most of the stars in the universe) through giants (which are most of the visible stars since dwarfs are dim). Stars may be on the main sequence where they fuse hydrogen into helium for most of their power, they may be red giants who have nearly exhausted their hydrogen, blue giants who are expending fuel at a spendthrift rate or they may be something more exotic.
Exotics stars include neutron stars (some of which are pulsars), white dwarfs, quasars, black holes and gamma ray bursters. Each of these exotic stars represent a different fate when stars leave the main sequence and begin to die. We are not going into details now, but they are interesting to everyone who is old enough to understand.
Basic astronomical physics consists of a relatively few items which generally go a fairly long way in answering questions raised at FDO. Towards the end of this section, I've tossed in some fairly heavy stuff - a bit of orbital mechanics and some stellar fusion. They are more for your interest than for you to try to teach someone else. Lets start with the real basics.
Everything that we can sense directly or through our instruments comes to us through one or more of the four fundamental forces of the universe. Three of the four have a major role in astronomy.
The nuclear force holds the nucleus of atoms together. Without the nuclear force there would be no atoms, no stars, no planets, no people, no matter and frankly no reason to bother with astronomy in the first place. The nuclear force is roughly a million times stronger than the electromagnetic force, but it has an minuscule range - about the size of a large atom's center. The nuclear force is transmitted by something called a gluon - the gismo which glues nuclei together.
The electromagnetic spectrum is almost everything we come in contact with in our daily lives. This force is why matter hangs together, it is radio, microwaves, heat, infrared radiation, visible light, ultraviolet radiation, x-rays, and the very energetic gamma rays. It is why rocks are hard, water is wet, air is a gas and just about everything that matters to you or me except gravity. The electromagnetic force is transmitted by something called a photon. A single photon is a particle of something in the electromagnetic spectrum. I will call that something "light", but you should remember that "light" includes not only visible light (red through violet), but all the invisible frequencies radio to infrared at longer frequencies and ultraviolet through gamma rays at short frequencies. Light has an infinite range.
Gravity is the third important force to astronomers. It is composed of hypothetical particles called gravitons. So far we have never actually detected a graviton or a gravity wave. Weirdly enough, the reason is that gravity is incredibly weak. It is some 1033 (billion trillion trillion) times weaker than the electromagnetic force. However, unlike the nuclear force which is extremely short ranged, and the electromagnetic force which while having an infinite range comes in positive and negative charges which cancel each other out, gravity only pulls. So even the weakest of forces when multiple trillions of atoms are involved add up to a very strong pull.
The last force - called the weak nuclear force, deals with certain types of radioactive decay. It is almost identical to the electromagnetic force except that instead of using a photon (which has an infinite range) it uses a meson which has a very short range - comparable to the range of the nuclear force. We won't consider it more.
It has been said that if you could take all the electric charges in 10 kilograms of matter (manifestations of the electromagnetic force) and place the positive ones on the Moon, and the negative ones on the Earth, the attractive force would pull the two together in short order. Yet all the gravitational force merely is enough to keep the Moon from wondering off and that is the result of the entire mass of the Earth. Actually, if you did split the charges and send positive charges to the Moon and left the negative ones here, nature would resolve the problem with a prodigious lightning bolt that would leave the Earth and hit the Moon.
Besides the four fundamental forces, the universe is composed of matter in a space and time matrix. The only matter we know is composed of atoms. There are speculations that other massive materials which do not interact (except gravitationally) with matter exist. Maybe, but this is still conjecture. We'll limit ourselves to matter formed of atoms. Matter comes in two basic forms - atoms with positively charged nuclei surrounded by a cloud of electrons (negative) and antimatter atoms with negatively charged nuclei and a cloud of positrons (positive). Matter and antimatter cannot survive in contact. The explosively merge yielding lots of highly energetic gamma rays. Maybe antimatter exists in bulk somewhere but we can't detect it.
In the universe, the 92 or so natural elements consist of more than 99.8% Hydrogen and Helium (the two lightest elements) and a trace of everything else. All the heavy complex atoms that we think of as normal are the rare exception to the rule. If we weigh all the detectable matter, it comes to a number which is about one tenth the amount needed to explain the force of gravity demonstrated by the speed at which galaxies turn. Whether the "missing matter" is in black holes, or halo stars we can't see because they are so dim, or some kind of exotic matter is a major question in astronomy and cosmology right now.
Stellar Fusion
In spite of the imposing sound of the title, the reactions inside stars really can be understood at a basic level without too much pain and suffering. Its outlined below. All this really says is that there are three basic ways that relatively stable stars can produce energy from fission: the annihilation of positrons, conversion of four hydrogen nuclei into a helium nuclei (in several alternative ways) and fusing three common helium nuclei forming carbon and eventually all the other atoms up to and including iron.
Proton Proton (Hydrogen Nuclei) Fusion Chains
 Before we attempt to use symbols to describe the proton proton fusion
cycle which dominates the production of power in the Sun, let see it pictorially. The
image shows electrons orbiting the atoms. This is "logically" correct (the electrons are
somewhere nearby) but an exaggeration because at temperatures of 15*106 K°
few if any electrons have not been stripped from the nucleus. Nuclei and free electrons
swarm about in a kind of a superhot broth called a plasma. A plasma differs from a gas in
that gasses are poor conductors of heat and electricity while plasmas are superlative
conductors - far better than the most conductive metals.
Before we attempt to use symbols to describe the proton proton fusion
cycle which dominates the production of power in the Sun, let see it pictorially. The
image shows electrons orbiting the atoms. This is "logically" correct (the electrons are
somewhere nearby) but an exaggeration because at temperatures of 15*106 K°
few if any electrons have not been stripped from the nucleus. Nuclei and free electrons
swarm about in a kind of a superhot broth called a plasma. A plasma differs from a gas in
that gasses are poor conductors of heat and electricity while plasmas are superlative
conductors - far better than the most conductive metals.
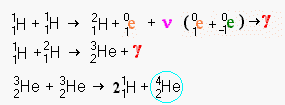 This pseudo mathematical
notation may look a little daunting but it really isn't too difficult to understand. In
fact it is just a symbolic version of what we saw pictorially above. We'll also learn
what all the little super and sub scripts mean, but they simply describe the diagram in
detail. In some of the examples below, you will come to a stage where two curved lines
leave a symbolic formula. This simply means there are two or more roads towards the
creation of normal helium after this stage. Some paths are shorter than others. Below we
will see that there are several ways to fuse hydrogen and get helium 4 as a result
including one roundabout path that creates beryllium, lithium and boron as an intermediate
stages.
This pseudo mathematical
notation may look a little daunting but it really isn't too difficult to understand. In
fact it is just a symbolic version of what we saw pictorially above. We'll also learn
what all the little super and sub scripts mean, but they simply describe the diagram in
detail. In some of the examples below, you will come to a stage where two curved lines
leave a symbolic formula. This simply means there are two or more roads towards the
creation of normal helium after this stage. Some paths are shorter than others. Below we
will see that there are several ways to fuse hydrogen and get helium 4 as a result
including one roundabout path that creates beryllium, lithium and boron as an intermediate
stages.
The first step in the process is the slowest. It takes an average of 14 billion years for two hydrogen nuclei to fuse at the temperatures in the Sun. At lower temperatures, such as the center of a red dwarf, this period become hundreds of billions and in a some cases trillions of years. At higher temperatures, the period shortens greatly until roughly 100 billion degrees when another system of fusion dominates. Bare hydrogen nuclei are very difficult to bring together because as the nuclei approach nearly dead on collisions won't swerve apart. At lower temperatures where the average speed of a particle is lower, there is more time to avoid a fusion so even a lower percentage of particles fuse. At higher speeds (i.e. higher temperatures), there is less time for the particles to sense each other and a slightly wider angle will allow a collision.
The Sun has been fusing hydrogen for roughly 5 billion years. This means that roughly 35% of the hydrogen should have been consumed and this is approximately what we measure in the Sun's spectrographs.
Once the two nuclei are fused, the result is an impossible nucleus which immediately throws out a neutrino and a positron (the anti particle equivalent to an electron). This changes one of the nucleons into a neutron, a chargeless particle which does not repel or attract charged particles. In the diagram, the positron is show meeting the now redundant second electron. In reality the positron will rapidly be attracted to any nearby electron. Since these are anti particles to each other they annihilate each other producing a power gamma ray (a form of electromagnetic energy far more violent than x-rays). The end of this operation is the heavy isotope of hydrogen that is often called deuterium.
Deuterium fuses at 8*106 K°. Brown dwarfs can generate a limited amount of fusion power from the traces of deuterium they contain even through they are two small to ignite normal hydrogen fusion. However in a hot environment like the Sun, deuterium is almost instantly fused with any nearby normal hydrogen nuclei. On average the lifetime of the deuterium created in the solar interior is about 6 seconds. The fusion of hydrogen and deuterium creates a light isotope of helium (helium 3) and more fierce gamma radiation.
The next stage of the fusion requires that two helium 3 nuclei meet each other. Since helium 3 nuclei are relatively rare in the swarm of hydrogen and helium 4 nuclei (which make up over 98.9 percent of the Sun), they are unlikely to meet soon. On average it takes about a million years for them to meet close enough to head on to fuse. The result of this fusion is a single nuclei of helium 4 plus two hydrogen nuclei left over. This may look like a little bit of magic, but the numbers all work out. A total of 6 hydrogen nuclei (protons) were used in the process in two sets of 3. Two protons were converted to neutrons, leaving two helium 3 nuclei (two protons and a neutron each). The final stage takes the pair of helium 3 nuclei, discards two protons and ends up with 2 protons and two neutrons creating normal helium 4.
It would seem that you could take a helium 3 nucleus, hit with a neutron creating a helium 4 nucleus directly. This can be done in the laboratory, but an unattached neutron is radioactively unstable. Within a halflife of 15 minutes it will spontaneously emit an electron become just another normal hydrogen nucleus. In a process with takes an average million years, no neutrons will be available when they decay so quickly. The second helium 3 nucleus is really just a carrier of a stabilized neutron. The two outside protons are just so much baggage to be discarded in the fusion once they cease to act as stabilizers for the neutron.
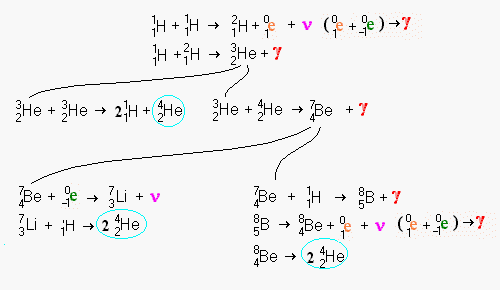 When a positron
(1e0) and a neutrino (ν) are created, the positron will instantly
encounter an electron (-1e0). Their mutual annihilation emits gamma
radiation (γ) The arrow symbol (→) when nothing is added to the left side
indicates radioactive decay.
When a positron
(1e0) and a neutrino (ν) are created, the positron will instantly
encounter an electron (-1e0). Their mutual annihilation emits gamma
radiation (γ) The arrow symbol (→) when nothing is added to the left side
indicates radioactive decay.
Notice the creation of beryllium on the longest changes followed by a radioactive decay back into helium. Beryllium is a very rare element simply because it is so fragile. Most elements which are multiples of alpha particles (i.e. helium nuclei) are among the most common elements (carbon, oxygen, magnesium, silicon, sulphur, and iron).
Carbon Cycle Fusion Chains
 This method of
producing helium from hydrogen is important in hot [108 K°] normal stars.
It uses carbon as a catalyst. Notice that the last step regenerates the carbon so that
the process will never run out of carbon. One of the points which is noticeable is that
every stage in this process creates energy. No of the stages fail to end up producing
gamma radiation.
This method of
producing helium from hydrogen is important in hot [108 K°] normal stars.
It uses carbon as a catalyst. Notice that the last step regenerates the carbon so that
the process will never run out of carbon. One of the points which is noticeable is that
every stage in this process creates energy. No of the stages fail to end up producing
gamma radiation.
The oxygen isotope with 15 nucleons is not the standard oxygen which has 16 nucleons (8 protons and 8 neutrons). The more common isotope of oxygen is formed when carbon and helium fuse in supernovae.
Triple Alpha (Helium Nuclei) Fusion Chain
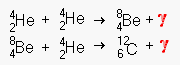 This is the fusion of
helium in extremely hot [108 K°] cores. Once the temperature reaches
this level, helium begins to fuse with beryllium to form carbon. Do not confuse this
relatively stable fusion process with the chaotic HELIUM FLASH that detonates a supernova.
Helium fusion can occur for millions of years in red supergiants.
This is the fusion of
helium in extremely hot [108 K°] cores. Once the temperature reaches
this level, helium begins to fuse with beryllium to form carbon. Do not confuse this
relatively stable fusion process with the chaotic HELIUM FLASH that detonates a supernova.
Helium fusion can occur for millions of years in red supergiants.
In extreme conditions leading to supernova, all sorts of secondary chains break out and all the elements up to 26Fe57 (the most stable and low energy isotope of iron) form. The elements above iron will not form by fusion since all these processes require the input of energy rather than outputting energy themselves. Only the additional shock of a supernova can create conditions where heavier elements form. Elements heavier than uranium quickly break down by radioactive decay, leaving the traditional 92 natural elements. [Francium is often counted as a natural element, but it is very unstable and not found naturally. Plutonium was once thought to exist only as a manufactured element, but minuscule traces have been found in various ores].
A single hydrogen atom weighs 1.00813 AMU [atomic mass units]. A single helium atom weighs 4.00389 AMU. Four hydrogen atoms combine to create a helium atom. However, 4*1.00813 (=4.03252) less 4.00389 leaves a residue of 0.02862 AMU. This 0.71% of the original mass has been converted to energy using Einstein's famous E=mc2 formula. For example, 1.0000 grams of hydrogen converted completely would yield 0.9939 grams of helium. Putting the missing 0.0071 grams into Einstein's formula we get
E = 0.0071grams * (29.97*109 centimeters/second)2 = 6.38*1018 ergs
Gamma radiation encounters countless atoms on the way to the surface of the star. As it ionizes atoms and is re-emitted in a cascade of lower frequency radiation (which in turn undergoes more cascading) the fierce gamma radiation descends the electromagnetic spectra becoming x-rays, UV light, light, IR light, microwaves, and finally various frequencies of radio.
The Sun's luminosity is 3.90*1033 ergs [gc2s-2] every second. For this luminosity, the Sun must convert 4.34*109 kilograms of mass to energy every second. This in turn requires 611*109 kilograms of hydrogen to become helium every second. The Sun weighs 199*1027 kilograms. The Sun has enough fuel to remain on the main sequence for about 7.5*109 years.
If you do the same sort of calculation for the conversion of potential energy to kinetic energy caused by gravity contracting the clouds the Sun formed from until it is squeezed as tightly as possible, you would only get enough energy to last 108 years. Nineteenth century physicists like Lord Kelvin figured that this was more than enough but this was before the age of the Earth was well understood. [We are about 5*109 years old already]. It wasn't until 1928 that nuclear reactions were well enough understood that we could assure ourselves that the stars were nuclear furnaces.
While about 97% of the energy emitted by the Sun comes from gamma rays, the neutrinos carry off a significant 3%. It is causing much consternation among astronomers and physicists that the predicted solar neutrino rate is less than 1%. Several theories exist which "explain" this disparity including neutrinos with non zero rest mass.
Some Useful Formulae
A few formulae from geometry will be useful later:
Volume of a sphere V = 4πr3 Area of a sphere A = 4/3πr2
