Resolution
Aperture Fever
Soon after an amateur astronomer gets really interested a dread debilitating condition overtakes him/her called aperture fever. Suddenly his/her lovely portable 100 millimeter telescope with GPS GOTO capabilities and diffraction limited optics just isn't enough. Stammering incoherently he/she tries to explain to his/her spouse why the both need to move to an area where there is room to place a 10 meter dome in the back yard to house a one meter telescope with all the neat feature already installed in the handy dandy 100 millimeter jewel.
In most such households the affronted spouse will retort that "You promised the 100 millimeter would be a big enough light bucket to see any star you were interested in." At this point the astronomer says "Oh, the telescope has plenty of light gathering ability but it doesn't have the necessary resolution. Resolution is the ability to distinctly see two distinct points as two points rather than one merged point of light." At which point the spouse asks the most dreaded word in human discourse "Why?".
Least Time Principle
In the interest of domestic tranquility, I'm about to try to answer that question. However much it may appear that I have started a random walk through obscure scientific facts, please bear with me. I'm peddling as fast as I can go in the direction of answering the resolution dilemma "Why do big scopes of equal quality invariably have better resolution than their smaller counterparts?".
I'll start with a little known but fascinating fact: "Light travels along the path which takes the least time to travel from the source to the target." This is called "Fermat's Principle". Now most of you know this character Fermat from his much more famous "Fermat's Lost Theorem" which conjectures [but does not prove] that a²+b²=c² is true for the exponent 2 and no other. Fermat may have thought he had a solution of the theorem but he really left it to Andrew Wile to prove it towards the end of the Twentieth Century. Likewise he correctly stated his principal on light propagation and left the proof of it to Twentieth Century quantum physicists like Richard Feynmann. In both cases, the proofs are so far beyond yours truly that I will simply state they have been proved correct and I don't know how. Like the salesman said "Trust me!" to which I will dutifully reply "Duhh.., OK."
How Fermat derived this formula empirically in 1650 is rather interesting. Hero of Alexander proposed that light travels along the shortest geometric path. This can be seen when light reflects from several mirrors properly arranged. The beam is also the shortest path that connects the mirrors the source and the target as long as the entire path is in the air. However if any part of the path travels through a material like glass or water which retards the speed of light, Fermat proposed that the actual path is such that the least time [not distance] is traveled.
Working on what seemed to be a separate problem, Claudius Ptolemy in 140 BC was trying to understand why and how much light bent as it traveled through differing transparent media. He developed a table which gave reasonably accurate results for air and water but did not work for any other materials like glass.
You might wonder why light doesn't simply travel along a straight line from the source to the target. Well in most cases where the media through which the light does not alter, and there is a direct path without something obscuring the source from the target, this shortest path is indeed the shortest time . The easiest way to show that this is not true is to notice that light travels slower through water than air. In fact it travels a lot slower through water than air. [Each transparent material has a unique number called the index of refraction which allow you to compare the relative time of travel through various materials. A vacuum [fastest] is 1.0, air is tiny fraction longer, water is 1.333, diamond is 2.42 and so on.]
 Consider a lifeguard who spots a swimmer in distress. How should the guard run and swim to minimize the time to reach the swimmer? If the guard heads straight to the swimmer along the red path, the distance will be minimal but if it takes the guard longer to swim ten yards than run ten yards, the time will not be minimal. If the guard minimizes the time swimming, along the blue path, an extra distance will have to be run. Again the blue path is not the least time. The green path which lies between the red and blue paths achieves the minimum time.
Consider a lifeguard who spots a swimmer in distress. How should the guard run and swim to minimize the time to reach the swimmer? If the guard heads straight to the swimmer along the red path, the distance will be minimal but if it takes the guard longer to swim ten yards than run ten yards, the time will not be minimal. If the guard minimizes the time swimming, along the blue path, an extra distance will have to be run. Again the blue path is not the least time. The green path which lies between the red and blue paths achieves the minimum time.
 How does this apply to light, well exactly the same thing applies. If a beam of light deep in a pool of water reaches an eye to the left and above it in the air the light path will follow the least time route, the green path. It does not travel along the red line (the shortest distance) nor the blue path (which minimizes the time in the water). You can observe this effect with a simple experiment. Place a pencil in a glass of water and observe it from various angles. You will notice that the pencil seems to bend at the interface between the water and the air.
How does this apply to light, well exactly the same thing applies. If a beam of light deep in a pool of water reaches an eye to the left and above it in the air the light path will follow the least time route, the green path. It does not travel along the red line (the shortest distance) nor the blue path (which minimizes the time in the water). You can observe this effect with a simple experiment. Place a pencil in a glass of water and observe it from various angles. You will notice that the pencil seems to bend at the interface between the water and the air.
All of this is a result of Snell's Law detailed in the FDO course materials.
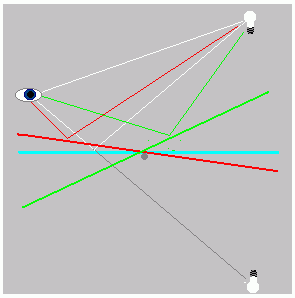 Consider the example at the left where you look at the reflection of a lamp in a mirror. Let us suppose that the mirror can pivot at the center. You may wish to actually try this experiment for yourself, but if not I'll describe what you will see. When the mirror is not tilted [light blue] the reflected image is formed on the other side of the mirror. Now ask yourself the question, "What is the shortest path in time for the reflection of the lamp to arrive at my eye after bouncing off the mirror?" If I didn't put in the restriction that the light had to bounce off the mirror, the answer would be the path directly connecting the eye and the lamp. Since the path in both cases is through air, the shortest path in time will also be the shortest path in distance. However I chose to determine the shortest total path, there will be a single spot on the mirror where this path touches. If I look at this spot I will see the reflected lamp.
Consider the example at the left where you look at the reflection of a lamp in a mirror. Let us suppose that the mirror can pivot at the center. You may wish to actually try this experiment for yourself, but if not I'll describe what you will see. When the mirror is not tilted [light blue] the reflected image is formed on the other side of the mirror. Now ask yourself the question, "What is the shortest path in time for the reflection of the lamp to arrive at my eye after bouncing off the mirror?" If I didn't put in the restriction that the light had to bounce off the mirror, the answer would be the path directly connecting the eye and the lamp. Since the path in both cases is through air, the shortest path in time will also be the shortest path in distance. However I chose to determine the shortest total path, there will be a single spot on the mirror where this path touches. If I look at this spot I will see the reflected lamp.
Now consider pivoting the mirror. Ask yourself the question "Will the image of the lamp move, and if so where and why?" Again the experiment is worthwhile, but the answer is simple. No matter which way you pivot the mirror, the image of the lamp will be on the spot of the mirror which minimizes the total path [in distance and hence in time]. If we pivot the mirror so that the near side approaches the eye [red], the lamp image will seem to move toward the left. If we pivot the mirror away from the eye [green], the image will move towards the right. It only takes a bit of geometry [or indeed a simple ruler] to convince yourself that in all cases, the total path length is minimized, and because we have light traveling through a single media, this means the total time is minimized.
Resolution of Optical Systems
We are ready to tackle the resolution problem now. We will assume for this argument that we have a "perfect optical system" with no flaws in the lens, no spherical nor chromatic aberrations. We will further assume that the seeing is perfect. There is no instability and clarity is as good as a vacuum. Couldn't we simply magnify the image enough that we could split the two points? The answer is no, there is a limit which cannot be exceeded. Many of you know rules of thumb such as 50 times the diameter measured in inches, but underlying such rules of thumb is Fermat's Principle.

Examine the diagram above. Two points (black and red) are being examined with some type of an optical device. I've shown this as a simplex convex lens, but it could be a mirror, or any of a number of other resolving systems (including microscopes). The distance of the two dots does not matter except that they are far enough that they might be difficult to resolve. For example the could be binary stars or two pin pricks in a sheet of aluminum foil a few dozen yards away. The principle remains the same. To make the diagram a little simpler I have shown the black dot perfectly aligned with the axis of the lens. This is not a requirement, but it reduces the problem to simply studying the red dot. Because the red dot is off center, it takes a slightly different amount of time for a photon to travel path t1 than t2. This means the time to reach the focal plane on the right side of the diagram is slightly different than each other.
The difference in these times (t1-t2) is crucial. Fermat's Principle is not exact. [Surprise, surprise, nothing from classical physics is exact, it seems, when laws are transported to the wonderful world of quantum mechanics.] Any two photons which arrive at the focus within a period of time which is less than or equal to the time required for a single wave crest to pass the focal point merge as if they were one. It does not matter how much you magnify these merged photons they still are one point. Now in the range of visual light, the time for a light wave to pass from one crest to another is very short. Light travels at 2.9979x108 meters per second. The distance between the crest of one wave of a photon and the next depends on the spectral color. Red photon have a wavelength of about 7.0x10-10 and violet light has a spectral length of about 4.0x10-10. These yield times of 2.335x10-18 seconds for red light and 1.334x10-18 second for violet light. If photons traveling the two paths have a difference in time which exceeds those very short time intervals, there is a theoretical possibility that you may be able to resolve them. Notice that you get better resolution at the violet end of the spectrum compared with the red end of the spectrum.
Consider the possibility of introducing a larger diameter objective. Because the objective is larger, the values of t1 and t2 increase and more important so does their difference. At some point as the objective becomes larger the difference will become great enough that it will exceed the time range. Notice also that as the wavelengths get larger, the time becomes longer. For AM radios frequencies, the interval is measured in millionths of a second rather than million million millionths of a second for light. This is why radio telescopes need to be so large to produce anything but the crudest maps of the sky.
There we have it. Somehow I'm not quite sure that all this dialog will ever persuade the spouse of our poor astronomer with aperture fever that selling house and home, moving to the western mountains and installing a meter sized light bucket makes sense, but at least both of them will know just why such a scope is needed.
If you wish to pursue this topic in more detail, I urge you to read Richard Feynmann's Lectures on Physics.